convert image from Cartesian to Polar-CodePudding

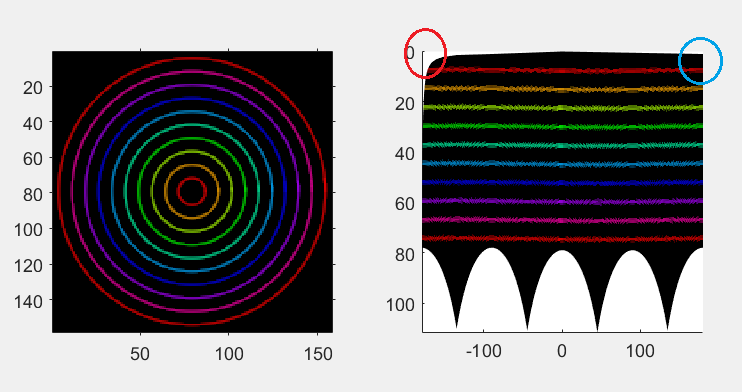
I want to convert an image from Cartesian to Polar and to use it for opengl texture. So I used matlab referring to the two articles below.

CodePudding user response：

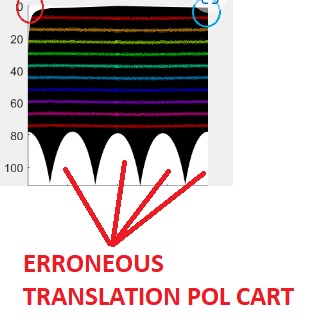
1.- The white arcs tell that the used translation pol-cart introduces significant errors.

2.- Reversing the following script solves your question.

It's a script that goes from cart-pol without introducing errors or ignoring input data, which is what happens when such wide white arcs show up upon translation apparently correct.

clear all;clc;close all

     clc,cla;
      format long;

      A=imread('shaffen dass.jpg');
      [sz1 sz2 sz3]=size(A);  
      szx=sz2;szy=sz1;
      A1=A(:,:,1);A2=A(:,:,2);A3=A(:,:,3);  % working with binary maps or grey scale images this wouldn't be necessary

      figure(1);imshow(A);
      hold all;
  Cx=floor(szx/2);Cy=floor(szy/2);
   plot(Cx,Cy,'co');                                                      % because observe image centre not centered

Rmin=80;Rmax=400;                                               % radius search range for imfindcircles
[centers, radii]=imfindcircles(A,[Rmin Rmax],...            % outer circle
    'ObjectPolarity','dark','Sensitivity',0.9);
h=viscircles(centers,radii);

hold all;                                                                  % inner circle
[centers2, radii2]=imfindcircles(A,[Rmin Rmax],...
    'ObjectPolarity','bright');
h=viscircles(centers2,radii2);

% L=floor(.5*(radii radii2));                                      % this is NOT the length X that should have the resulting XY morphed graph
L=floor(2*pi*radii);                                                           % expected length of the morphed graph

cx=floor(.5*(centers(1) centers2(1)));                      % coordinates of averaged circle centres
cy=floor(.5*(centers(2) centers2(2)));

plot(cx,cy,'r*');                                                        % check avg centre circle is not aligned to figure centre
plot([cx 1],[cy 1],'r-.');

t=[45:360/L:404 1-360/L];                                                       % if step=1 then we only get 360 points but need an amount of L points
                                                                                % if angle step 1/L over minute waiting for for loop to finish
R=radii 5;x=R*sind(t) cx;y=R*cosd(t) cy;                  % build outer perimeter
hL1=plot(x,y,'m'); % axis equal;grid on;  

% hold all;
% plot(hL1.XData,hL1.YData,'ro');

x_ref=hL1.XData;y_ref=hL1.YData;

% Sx=zeros(ceil(R),1);Sy=zeros(ceil(R),1);
Sx={};Sy={};

for k=1:1:numel(hL1.XData)
    Lx=floor(linspace(x_ref(k),cx,ceil(R)));
    Ly=floor(linspace(y_ref(k),cy,ceil(R)));
    % plot(Lx,Ly,'go');    % check
    % plot([cx x(k)],[cy y(k)],'r');
%     L1=unique([Lx;Ly]','rows');
    Sx=[Sx Lx'];Sy=[Sy Ly'];
end

sx=cell2mat(Sx);sy=cell2mat(Sy);

[s1 s2]=size(sx);

B1=uint8(zeros(s1,s2));
B2=uint8(zeros(s1,s2));
B3=uint8(zeros(s1,s2));

for n=1:1:s2
    for k=1:1:s1
        B1(k,n)=A1(sx(k,n),sy(k,n)); 
        B2(k,n)=A2(sx(k,n),sy(k,n)); 
        B3(k,n)=A3(sx(k,n),sy(k,n)); 
    end
end

C=uint8(zeros(s1,s2,3));
C(:,:,1)=B1;
C(:,:,2)=B2;
C(:,:,3)=B3;
figure(2);imshow(C);

the resulting

3.- let me know if you'd like some assistance writing pol-cart from this script.

Regards

John BG

CodePudding user response：

Those issues you show in your question happen because your algorithm is wrong.

What you did (push):

throw a grid on the source image
transform those points
try to plot these colored points and let MATLAB do some magic to make it look like a dense picture

Do it the other way around (pull):

throw a grid on the output
transform that backwards
sample the input at those points

The distinction is called "push" (into output) vs "pull" (from input). Only Pull gives proper results.

Very little MATLAB code is necessary. You just need pol2cart and interp2, and a meshgrid.

With interp2 you get to choose the interpolation (linear, cubic, ...). Nearest-neighbor interpolation leaves visible artefacts.

im = im2single(imread("PQFax.jpg"));

% center of polar map, manually picked
cx = 10   409/2;
cy = 7   413/2;

% output parameters
radius = 212;
dRho = 1;
dTheta = 2*pi / (2*pi * radius);
Thetas = pi/2 - (0:dTheta:2*pi);
Rhos = (0:dRho:radius);

% polar mesh
[Theta, Rho] = meshgrid(Thetas, Rhos);

% transform...
[Xq,Yq] = pol2cart(Theta, Rho);

% translate to sit on the circle's center
Xq = Xq   cx;
Yq = Yq   cy;

% sample image at those points
Ro = interp2(im(:,:,1), Xq,Yq, "cubic");
Bo = interp2(im(:,:,2), Xq,Yq, "cubic");
Go = interp2(im(:,:,3), Xq,Yq, "cubic");
Vo = cat(3, Ro, Bo, Go);
Vo = imrotate(Vo, 180);
imshow(Vo)

The other way around (get a "torus" from a "ribbon") is quite similar. Throw a meshgrid on the torus space, subtract center, transform from cartesian to polar, and use those to sample from the "ribbon" image into the "torus" image.

I'm more familiar with OpenCV than with MATLAB. Perhaps MATLAB has something like OpenCV's warpPolar(), or a generic remap(). In any case, the operation is trivial to do entirely "by hand" but there are enough supporting functions to take the heavy lifting off your hands (interp2, pol2cart, meshgrid).