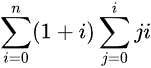If I have some double summation like this, how do I completely vectorize it? (No loops)

A good starting point would be to get vector i and j. For example if n = 2:

i = 0:2
j = c(0,0,1,0,1,2)

Then how should we approach next?

CodePudding user response：

1. i = 0 and j = 0 contribute nothing, so the summation can start from 1, not 0;

2. outer can be used to evaluate j * i * (i 1) for all i = 1, 2, ..., n and j = 1, 2, ..., n, giving an n-by-n square matrix;

3. the summation is over j <= i, only involving elements in the lower triangular part of this matrix.

n <- 2
i <- 1:n
j <- 1:n
x <- outer(i, j, function (i, j) j * i * (i   1))
sum(x[lower.tri(x, diag = TRUE)])
#[1] 20

A less intuitive but more efficient way is to generate (i, j) index for all the lower triangular elements directly.

n <- 2
i <- sequence(n:1, 1:n)
j <- rep(1:n, n:1)
sum(j * i * (i   1))
#[1] 20

Actually, after some simple math, I realize that this simplifies to a single summation:

n <- 2
i <- 1:n
0.5 * c(crossprod(i * (i   1)))
#[1] 20

CodePudding user response：

1) Use row and col to get matrices i and j and then just write out the formula multiplying by the inequality shown to zero out the cells above the diagonal.

n <- 2
i <- row(diag(n 1)) - 1
j <- col(i) - 1
sum( (i 1) * i * j * (j <= i) )
## [1] 20

2) Since the zero row and column don't actually contribute to the sum we could alternately use:

n <- 2
i <- row(diag(n))
j <- col(i)
sum( (i 1) * i * j * (j <= i) )
# [1] 20

3) Another approach which builds on the former approaches is that it is clear that the result is a polynomial in n. Try a number of different degree until we find the smallest degree that gives zero residuals to the following regression and then use that to generate the answer. We found that to be 5 so encoding (2) in f we calculate fm once and from then on we only need the predict line.

f <- function(n, i = row(diag(n)), j = col(i)) sum( (i 1) * i * j * (j <= i) )
fm <- lm(v ~ poly(n, 5), data.frame(v = sapply(1:10, f), n = 1:10))

# test - calculate sum for n = 2
unname(predict(fm, list(n = 2)))
## [1] 20

Check

To double check this we can use list comprehensions to get a direct translation to code.

library(listcompr)

sum( gen.vector((i   1) * i * j, j <= i, i = 0:n, j = 0:n) )
## [1] 20