Generate linear fit samples using the standard errors from scipy.stats.linregress-CodePudding

I'm using

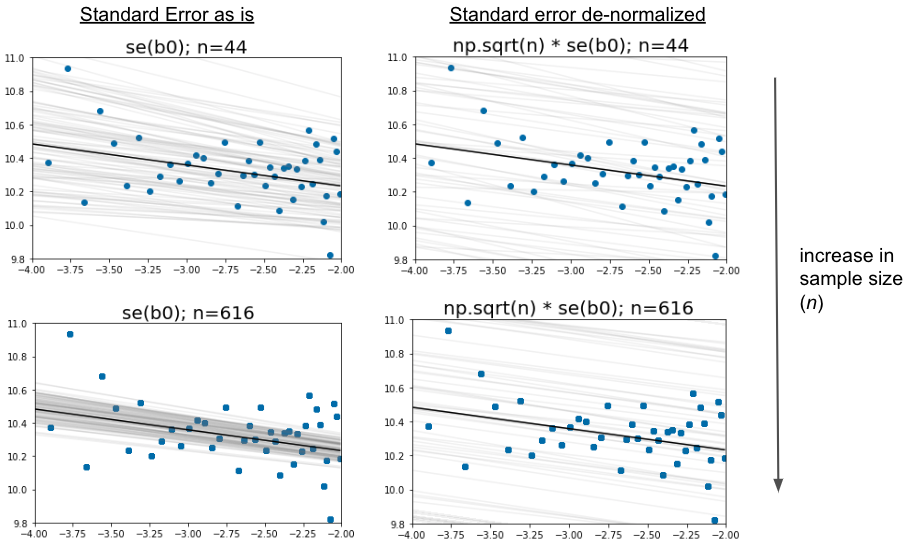
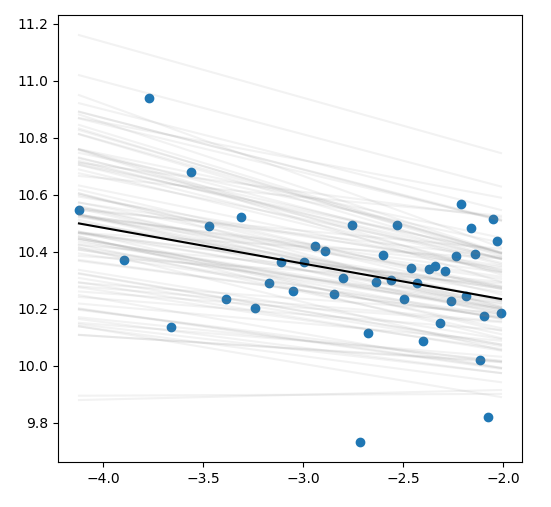
My question is: given that stderr and intercept_stderr are standard errors and numpy.random.normal expects standard deviations, should I multiply stderr and intercept_stderr by $\sqrt{N}$ when sampling?

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

x = np.array([-4.12078708, -3.89764352, -3.77248038, -3.66125475, -3.56117129,
       -3.47019951, -3.3868179 , -3.30985686, -3.2383979 , -3.17170652,
       -3.10918616, -3.05034566, -2.99477581, -2.94213208, -2.89212166,
       -2.84449361, -2.79903124, -2.75554612, -2.71387343, -2.67386809,
       -2.63540181, -2.59836054, -2.56264246, -2.52815628, -2.49481986,
       -2.462559  , -2.43130646, -2.40100111, -2.37158722, -2.34301385,
       -2.31523428, -2.28820561, -2.2618883 , -2.23624587, -2.21124457,
       -2.18685312, -2.16304247, -2.13978561, -2.11705736, -2.09483422,
       -2.07309423, -2.05181683, -2.03098275, -2.01057388])
y = np.array([10.54683181, 10.37020828, 10.93819231, 10.1338195 , 10.68036321,
       10.48930797, 10.2340761 , 10.52002056, 10.20343913, 10.29089844,
       10.36190947, 10.26050936, 10.36528216, 10.41799894, 10.40077834,
       10.2513676 , 10.30768792, 10.49377725,  9.73298189, 10.1158334 ,
       10.29359023, 10.38660209, 10.30087358, 10.49464606, 10.23305099,
       10.34389097, 10.29016557, 10.0865885 , 10.338077  , 10.34950896,
       10.15110388, 10.33316701, 10.22837808, 10.3848174 , 10.56872297,
       10.24457621, 10.48255182, 10.39029786, 10.0208671 , 10.17400544,
        9.82086658, 10.51361151, 10.4376062 , 10.18610696])

res = stats.linregress(x, y)

s_vals = np.random.normal(res.slope, res.stderr, 100)
i_vals = np.random.normal(res.intercept, res.intercept_stderr, 100)
for i in range(100):
    plt.plot(x, i_vals[i]   s_vals[i]*x, c='grey', alpha=.1)

plt.scatter(x, y)
plt.plot(x, res.intercept   res.slope*x, c='k')
plt.show()

CodePudding user response：

TL;DR

Indeed, it is an estimate of the standard deviation since standard error means standard deviation of the error of a particular parameter. No, there is no need to "de-normalize" by multiplying with np.sqrt(n). Finally, however, you might want to change the distribution from which you sample the simulated parameters with that of a