I'm given three GPS points for instance in terms of their geocoordinates (longitude, latitude) that are relatively close to each other:
p1 = (p1_lon, p1_lat)
p2 = (p2_lon, p2_lat)
p3 = (p3_lon, p3_lat)
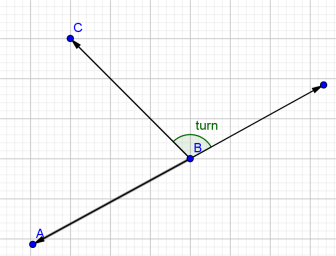
Suppose a path exists from p1 to p2 (called segment C), then p2 to p3 (called segment A). Then suppose I draw a direct line from p1 to p3 (called segment B). How can I compute for the turn angle? Is that the angle formed between segments C and A (i.e., opposite segment B). Or should I subtract this angle from 180 degrees (or np.pi radians) to obtain the turn angle?
Also, in terms of computing for the aforementioned angle, I assume that the Law of Cosines for Triangles is required?
B**2 = A**2 C**2 - 2*A*C*cos(theta)
where theta is the angle that we are solving. So rearranging the equation, we get:
theta = np.arccos((B**2 - A**2 - C**2)/(-2*A*C))
But I'm getting nan. I'm led to believe that using cosine or inverse cosine is problematic especially for small distances/angles. I'm currently using the geodesic distance which I thought is the most accurate distances when measuring distance between two geocoordinates. I think I read somewhere about haversine distance? But I'm not sure what it is and if it is accurate to use for measuring distances. Will it help in calculating the theta much easily and faster avoiding the nans. Any advice is greatly appreciated. Thank you.
CodePudding user response:
You need to calculate azimuth a21 from p2 to p1 (note it is not the same as azimuth from p1 to p2!), then azimuth a23 from p2 to p3, then calculate turn angle as
turn = a32 - (a21 180)
and correct it to range 0..360 or -180..180 if needed (adding/subtracting 360)
Form moving A-B-C and turn after B:
To get azimuth, you can use appropriate Python geolibrary - I see that geographiclib contains it.
CodePudding user response:
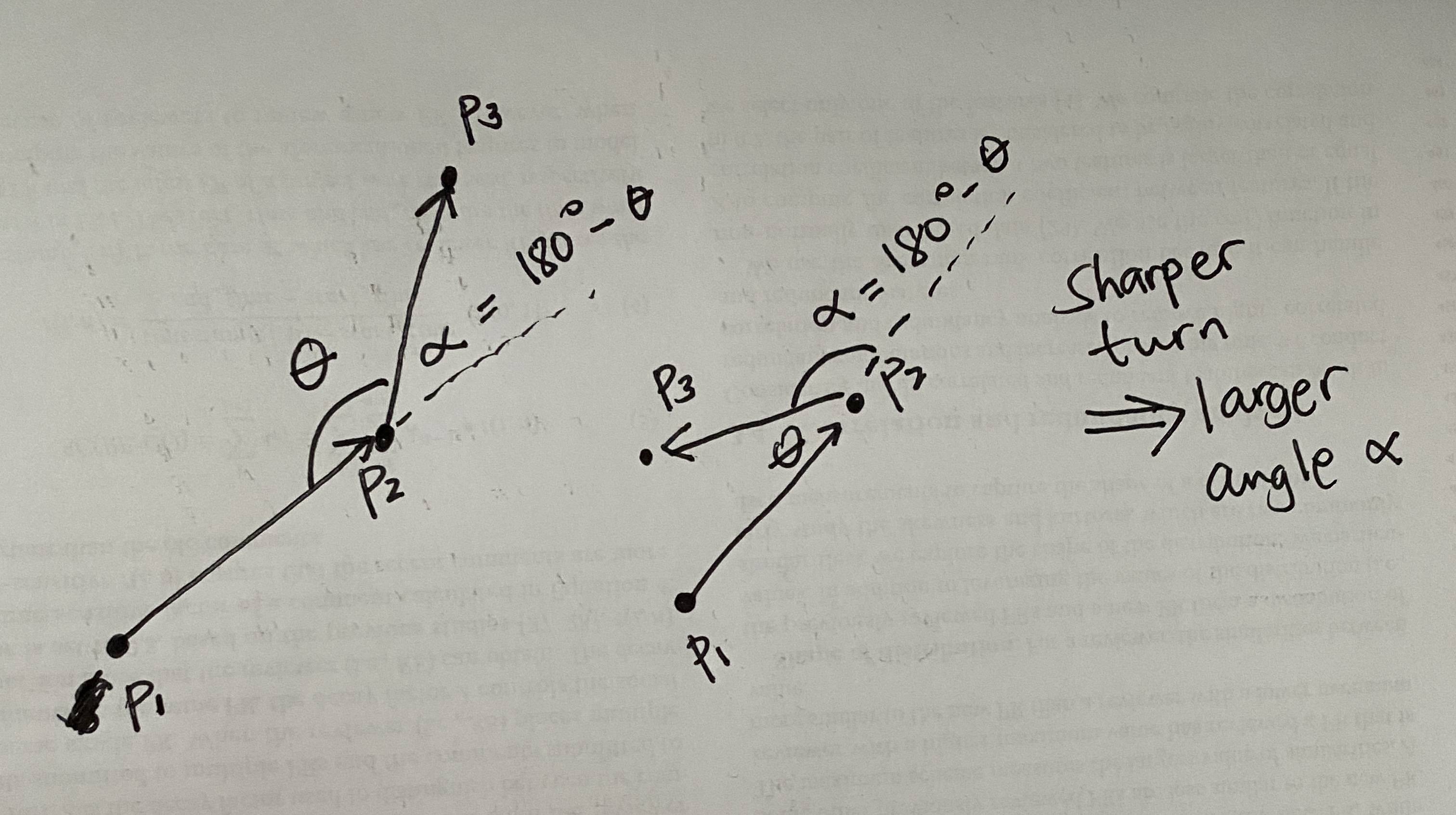
@MBo I think I should have drawn a picture in the first place. Anyways, I drew a picture of what I mean. theta here is the angle formed with segment p1 to p2 when the object moves from p2 to p3. It also occurred to me that a sharper turn induces a larger turning angle alpha (second case) while the first case should only have smaller turning angle as the turn is not that sharp compared to the second one. So I believe we can compute alpha by subtracting 180 degrees minus the theta (this makes sense because if p1 and p3 form a straight line with p2 on that line, i.e. the points are collinear with p2 in the middle of the other two points, then the object went straight direction from p2 so the turn angle is 0 degrees; and if they are all collinear still but either p1 or p3 is in the middle of p2 and p3 or p1, then we'll know the object went backwards and so the turn is 180 degrees). This should all happen symmetrically as well on the other side. Clearly, the turn angles can only be between [0,180].
The problem then arises with calculating theta. Because the three points are GPS coordinates and very small, the angle can be small as well. And thus applying the cosines/arccosines can be ill-conditioned as some articles I've read online suggest. I'm not sure what is a turn around for this. Can I compute such angles without having to use the cosines/arccosines? And when you mentioned about azimuth, did you mean I have to compute it and use it? Why would we need it and how can it help in the problem?