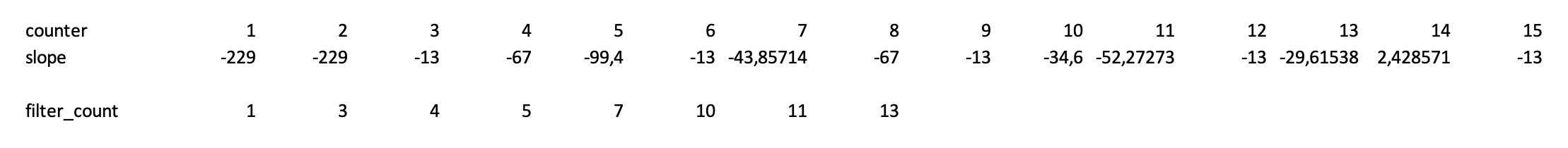(Disclaimer: not a good programmer, so I apologise in advance if my language is not precise.)

I have two list, and I want to identify all the items in the second list ("slope") that are smaller than -1, and does not have a previous duplicate. Then I wish to return the corresponding items in the first list (counter) where these two if-condition are met. (New list: "filter_count".)

This line of code does the job:

filter_count = [i for i,j in zip(counter, slope) if i-1 == slope.index( slope[int(i-1)] ) and j<=-1]

But when I am using the timer function between each of my line of code I see that the whole script use around 13 seconds to compute, but this specific line of code use around 99,9% of all the time! In other words, I assume I have written an extremely inefficient line here and wonder if I could do it much easier.

For reference, this is an example on how the filter_count should be with these lists (in my real example it is much much longer)

CodePudding user response：

Use the dictionary to record the index of the first occurrence of each element, and then traverse to get the result:

>>> mapping = {}
>>> for i, elem in zip(counter, slope):    # or enumerate(slope, 1)
...     mapping.setdefault(elem, i)
...
>>> [i for elem, i in mapping.items() if elem < -1]
[1, 3, 4, 5, 7, 10, 11, 13]

Note: it depends on the dictionary ensure the insertion order in Python 3.7 . If you are using an earlier Python version, consider using collections.OrderedDict, or using set and list together.

CodePudding user response：

Using set to prevent previous duplicate

counter = list(range(1, 16))
slope = [-229, -229, -13, -67, -99.4, -13, -43.8, -67, -13, -34.6, -52.2, -13, -29.6, 2.4, -13]
s = set()
filter_count = []
for i, e in zip(counter, slope):
    if e not in s and e < 0:
        s.add(e)
        filter_count.append(i)

print(filter_count)

Prints:

[1, 3, 4, 5, 7, 10, 11, 13]

CodePudding user response：

UPDATED: (larger test lists)

The issue is that you are doing an index search for every element. This means the complexity of your algorithm is O(n²).

The set and dict solutions are better because they trade off memory to gain speed. Here is a very crude quick script for comparing the performance:

import sys
from timeit import timeit


def generate_list(size: int) -> list:
    return list(range(-size//2, size//2))


def original_solution(counter: list, slope: list) -> list:
    filter_count = [i for i, j in zip(counter, slope) if i-1 == slope.index(slope[int(i-1)]) and j <= -1]
    return filter_count


def using_dictionary(counter: list, slope: list) -> list:
    """Inspired by Mechanic Pig"""
    mapping = {}
    for i, elem in zip(counter, slope):
        mapping.setdefault(elem, i)
    filter_count = [i for elem, i in mapping.items() if elem < -1]
    return filter_count


def using_set(counter: list, slope: list) -> list:
    """Inspired by Алексей Р"""
    s = set()
    filter_count = []
    for i, e in zip(counter, slope):
        if e not in s and e < 0:
            s.add(e)
            filter_count.append(i)
    return filter_count


def main():
    size, n = sys.argv[1:]
    print(f"List size: {size}, n: {n}")
    print("Time in seconds:")
    for func in [original_solution, using_dictionary, using_set]:
        name = func.__name__
        t = timeit(
            f'counter = slope = generate_list({size}); '
            f'{name}(counter, slope)',
            setup=f'from __main__ import generate_list, {name}',
            number=int(n)
        )
        print(f'{name:<18}', round(t, 4))


if __name__ == '__main__':
    main()

You can call the script providing the desired list size and number or repetitions.

python test_script.py 10000 10

The results:

List size: 10000, n: 10
Time in seconds:
original_solution  3.5511
using_dictionary   0.0122
using_set          0.0093

I would speculate that the set solution is slightly better because both adding and lookup are O(1) in complexity and there is only one loop, making the entire algorithm O(n).

While the dict solution is technically also O(n), it has to do two loops, meaning 2 * n iterations in practice. So in the limit it is the same as the set solution, but in practice it will probably always be a bit slower.

CodePudding user response：

This solution does not give the exact same result but still returns the index of each unique value. For example in case of the 1, 2 pair it returns 2 instead of 1 as it does in your result. Therefore still meets the requirements.
If you wanted the exact same result, you'd need to create a temporary dictionary (with index: val) and reverse the order before creating slope_d (val: index).

# create list for testing
slope = [-229, -229, -13, -67, -99.4, -13, -43.85, -67, -13, -34.6, -52.27, -13, -29.61, 2.42, -13]

# transform to a dict with the values as keys
slope_d = {val: idx 1 for idx, val in enumerate(slope) if val <= -1}
# here lies the trick: since the keys of a dict are unique, 
# they will be overwritten if there's the same value present in the original list

# transform to list for output
filter_count = list(slope_d.values())
filter_count.sort()

print(filter_count)

Result:

[2, 5, 7, 8, 10, 11, 13, 15]

CodePudding user response：

Try this

filter_count = [
    count for i, count in enumerate(counter)
    if slope[i]<-1 and count not in counter[:i]
]