For years I have been annoyed with the returning task of having to set up playgroups for my kids classes. Now having 3 kids this task is a bit daunting. Hence, great if an automatization can be implemented.
Below is the problem for one of the classes, great if it can be more flexible regarding number of participants, groups and occurrences.
Information:
- Playgroups will occur 10 times during a year
- Playgroups will be reshuffled for each occurrence
- Participant pool is: - 9 boys - 12 girls
- Create 5 groups with 4-5 participants for each Playgroup occurrence
- Minimum 2 boys and 2 girls in each group
- If the minimum cannot be achieved, then only one sex is a group (in this case there will be a girls group of 4 participants)
- Optimal solution will have fewest overlap of participants across occurrences.
I have a preference for the solution / toolbox to be in excel (with VBA if needed).
CodePudding user response:
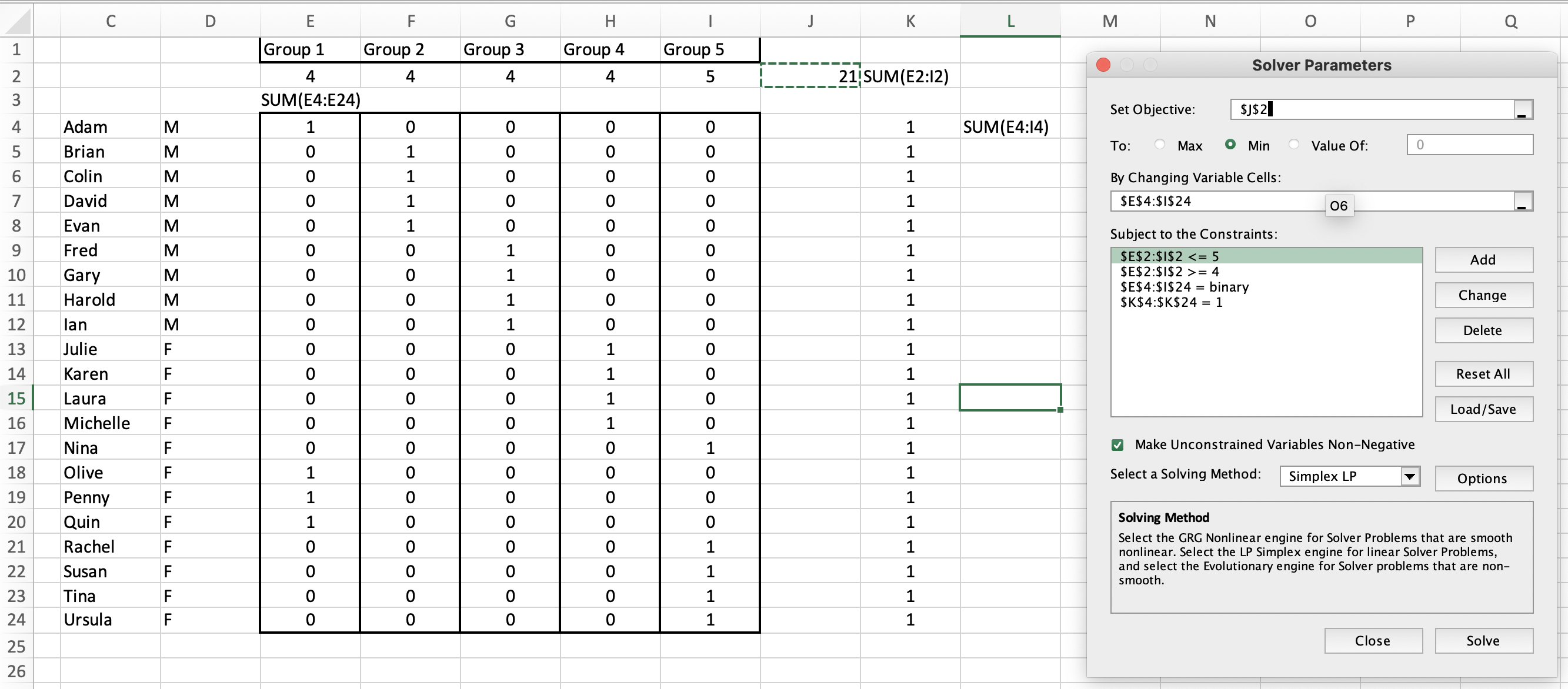
Well, set this up as a basic control. You can add extra constraints as you need, such as controlling the number of M and F in each group, be good practice for you.
CodePudding user response:
I don't think this is really an excel or vba question, more of a general question about an algorithm. The problem you describe is non-trivial and related to the social golfer problem which has been proven to be NP-complete, so very difficult to solve for larger amounts of people/groups.
For your parameters, the social golfer problem in its original form (no two people can ever be in the same group twice) is obviously unsolvable, so you have to specify what you want "minimum overlap" to mean. It can either mean "maximize the number of overall contacts" so every child should be in the same group with every other child at least once. This seems achievable pretty easily with your parameters.
Alternatively you can try to minimize a "penalty score" aka each child should be in the same group as every other child as least once, but not more than once. Being in the same group more than twice will increase the "penalty score" which you try to minimize. This is certainly a valid option for your problem.
Luckily there is a website that allows you to determine a schedule just like this, however, it can't fulfill your requirement of an even boy/girl distribution. The website can be found here: https://goodenoughgolfers.com/
I once wrote a solver for this problem myself, including the boy/girl distribution requirement, but it is still very bare bone and just available as source code in c here.
I computed the following distributions with my tool and adapted the result manually to fit your criteria:
Day 1
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 |
|---|---|---|---|---|
| Boy 1 | Boy 2 | Boy 3 | Boy 4 | |
| Boy 6 | Boy 7 | Boy 8 | Boy 9 | |
| Boy 5 | ||||
| Girl 1 | Girl 2 | Girl 3 | Girl 4 | Girl 5 |
| Girl 7 | Girl 8 | Girl 9 | Girl 10 | |
| Girl 11 | Girl 12 | |||
| Girl 6 |
Day 2
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 |
|---|---|---|---|---|
| Boy 1 | Boy 9 | Boy 4 | ||
| Boy 3 | Boy 5 | |||
| Boy 6 | Boy 8 | Boy 7 | Boy 2 | |
| Girl 9 | Girl 2 | Girl 12 | ||
| Girl 5 | Girl 4 | Girl 10 | ||
| Girl 3 | Girl 11 | Girl 8 | Girl 7 | Girl 6 |
| Girl 1 |
Day 3
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 |
|---|---|---|---|---|
| Boy 8 | Boy 5 | Boy 9 | ||
| Boy 3 | Boy 6 | Boy 1 | Boy 7 | |
| Boy 4 | Boy 2 | |||
| Girl 3 | ||||
| Girl 9 | Girl 12 | Girl 8 | Girl 7 | Girl 5 |
| Girl 6 | Girl 2 | Girl 1 | Girl 10 | Girl 4 |
| Girl 11 |
Day 4
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 |
|---|---|---|---|---|
| Boy 5 | ||||
| Boy 9 | Boy 1 | Boy 8 | Boy 6 | |
| Boy 2 | Boy 3 | Boy 4 | Boy 7 | |
| Girl 12 | Girl 1 | Girl 10 | Girl 2 | Girl 6 |
| Girl 3 | Girl 8 | Girl 11 | Girl 9 | |
| Girl 4 | Girl 5 | |||
| Girl 7 |
Day 5
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 |
|---|---|---|---|---|
| Boy 5 | Boy 3 | Boy 7 | Boy 6 | |
| Boy 9 | Boy 1 | Boy 8 | ||
| Boy 4 | Boy 2 | |||
| Girl 5 | Girl 9 | Girl 3 | Girl 11 | |
| Girl 4 | Girl 2 | Girl 10 | Girl 1 | |
| Girl 8 | Girl 12 | Girl 7 | ||
| Girl 6 |
Day 6
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 |
|---|---|---|---|---|
| Boy 8 | Boy 4 | Boy 2 | ||
| Boy 5 | Boy 3 | Boy 1 | Boy 6 | |
| Boy 7 | Boy 9 | |||
| Girl 9 | Girl 8 | Girl 6 | Girl 5 | |
| Girl 3 | Girl 10 | Girl 7 | ||
| Girl 12 | Girl 1 | Girl 11 | Girl 4 | |
| Girl 2 |
Day 7
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 |
|---|---|---|---|---|
| Boy 2 | Boy 3 | Boy 7 | ||
| Boy 8 | Boy 4 | Boy 1 | ||
| Boy 6 | Boy 9 | Boy 5 | ||
| Girl 9 | Girl 8 | Girl 1 | Girl 4 | |
| Girl 5 | Girl 10 | |||
| Girl 3 | Girl 7 | Girl 2 | Girl 6 | Girl 12 |
| Girl 11 |
Day 8
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 |
|---|---|---|---|---|
| Boy 5 | Boy 7 | Boy 8 | Boy 4 | |
| Boy 2 | Boy 1 | Boy 3 | ||
| Boy 9 | Boy 6 | |||
| Girl 1 | Girl 12 | Girl 7 | Girl 10 | Girl 11 |
| Girl 5 | Girl 2 | |||
| Girl 3 | Girl 8 | Girl 9 | Girl 6 | |
| Girl 4 |
Day 9
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 |
|---|---|---|---|---|
| Boy 6 | Boy 7 | Boy 9 | ||
| Boy 1 | Boy 3 | Boy 4 | ||
| Boy 8 | Boy 2 | Boy 5 | ||
| Girl 6 | Girl 2 | Girl 1 | ||
| Girl 10 | Girl 8 | Girl 7 | Girl 12 | |
| Girl 4 | Girl 9 | Girl 3 | Girl 5 | |
| Girl 11 |
Day 10
| Group 1 | Group 2 | Group 3 | Group 4 | Group 5 |
|---|---|---|---|---|
| Boy 4 | Boy 6 | Boy 1 | Boy 2 | |
| Boy 7 | Boy 5 | Boy 3 | ||
| Boy 9 | Boy 8 | |||
| Girl 12 | Girl 2 | Girl 7 | ||
| Girl 5 | Girl 8 | Girl 3 | ||
| Girl 11 | Girl 9 | Girl 10 | Girl 6 | Girl 1 |
| Girl 4 |