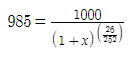I was searching for some way to use Sympy in R, but I didn't find anything that could solve the equation below without errors.
Is is actually possible to use something like Sympy in R?
CodePudding user response:
There are several packages at CRAN that may help:
They may all have different levels of difficulty in terms installing the underlying 'engine' but this should get you started.
CodePudding user response:
It will definitely be easiest to do this numerically, if you can live with that:
uniroot(function(x) 1000/(1 x)^(25/252) - 985, c(0,10))
However: I tried this in Wolfram Alpha, which gave me the exact result
x = (102400000000000000000000 2^(6/25) 5^(4/25) 197^(23/25) -
17343170265605241347130653)/17343170265605241347130653
and then moments later reverted to giving me the numerical approximation (x ≈ 0.164562) -- I had to quickly copy the text before it disappeared.
When I tried this with sympy, it quickly gave me a numerical answer:
from sympy import *
x = Symbol("x")
solve(1000/((1 x)**(25/252)) - 985, x)
[0.164562487329317]
... but trying to get an exact solution by setting numerical = False was no good: it seemed to have to work fairly hard (pegged CPU at 100% for several minutes before I gave up). This is consistent with my results from Ryacas,
library(Ryacas)
yac("Solve(1000/((1 x)^(25/252)) == 985, x)")
Error in yac_core(x) : Yacas returned this error: CommandLine(1) : Max evaluation stack depth reached. Please use MaxEvalDepth to increase the stack size as needed.
However, there is a surprising shortcut. The hard part of this problem is actually doing the deep recursion needed to unravel the (25/252) power exactly. If you're happy with a more general solution, you can get it quickly:
In sympy:
a = Symbol("a")
solve(1000/((1 x)**(a)) - 985, x, numerical = False)
[-1 200**(1/a)/197**(1/a)]
This works in caracas (an R wrapper for sympy) too, once everything is set up:
library(caracas)
x <- symbol('x')
a <- symbol('a')
solve_sys(1000/((1 x)^a), 985, list(x))
## Solution 1:
## x = -1
## ───
## a a _____
## -1 197 ⋅╲╱ 200
Unfortunately, the same trick doesn't seem to work for Ryacas.