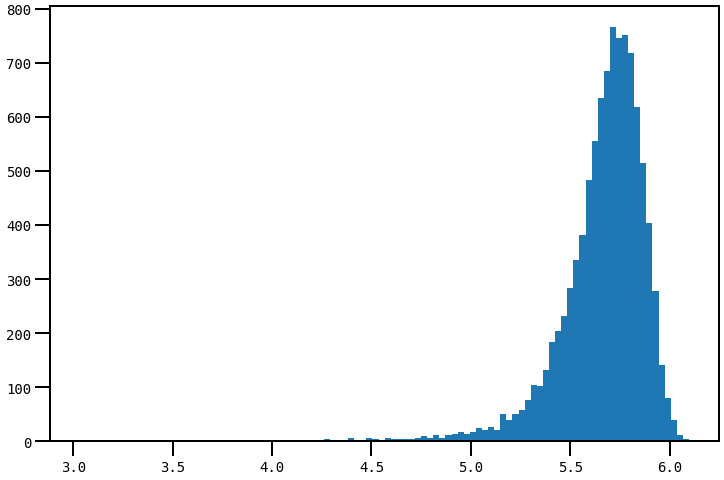
Consider

xdata=np.random.normal(5e5,2e5,int(1e4))
plt.hist(np.log10(xdata), bins=100)
plt.show()
plt.semilogy(xdata)
plt.show()

is there any way to display xticks of the first plot (plt.hist) as in the second plot's yticks? For good reasons I want to histogram the np.log10(xdata) of xdata but I'd like to set minor ticks to display as usual in a log scale (even considering that the exponent is linear...)

In other words, I want the x_axis of this plot:

to be like the y_axis

of the 2nd plot, without changing the spacing between major ticks (e.g., adding log marks between 5.5 and 6.0, without altering these values)

CodePudding user response：

yes you need to set the axes as log

ax = plt.gca()  # get current axes
ax.set_yscale("log")

EDIT

Please note that plt module has not method set_yscale, if you don't want to recover the axes and alternative can be:

fig, ax = plt.subplots()
plt.hist(xdata) # equivalent to ax.hist(xdata)
ax.set_yscale("log")
plt.show()

CodePudding user response：

Just kept for now for clarification purpose. Will be deleted when the question is revised.

Disclaimer:

• As

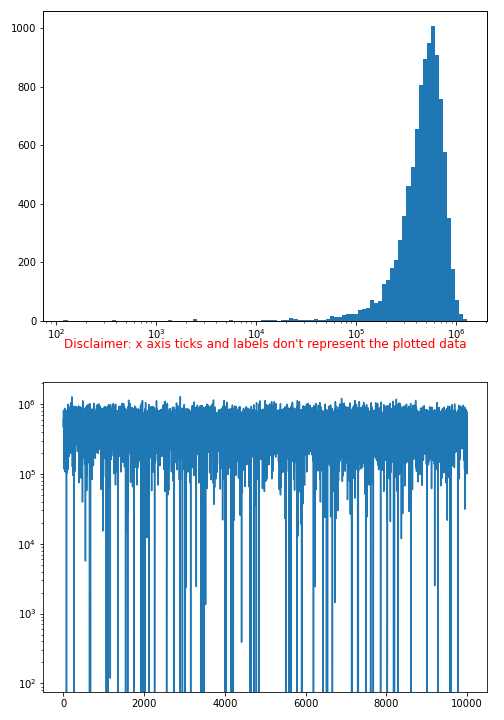
  Explanation how that special axis transfer plot is done:

  • original x-axis is hidden
  • a

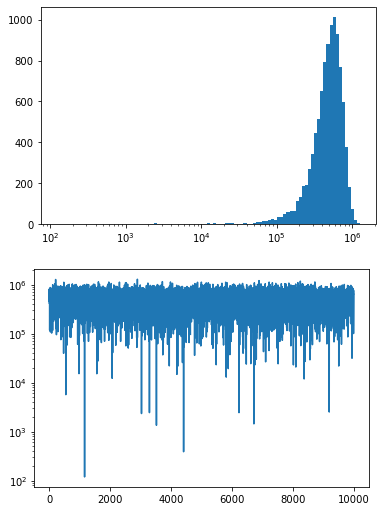
    Explanation:

    1. Cut off negative values
       • The randomly generated example data likely contains still some negative values
         • activate the commented code lines at the beginning to see the effect
       • logarithmic function isn't defined for values <= 0
         • while the 2nd plot just deals with y-axis log scaling (negative values are just out of range), the 1st plot doesn't work with negative values in the BINs range
       • probably real world working data won't be <= 0, otherwise keep that in mind
    2. BINs should be aligned to log scale as well
       • otherwise the 'BINs widths' distribution looks off
         • switch # on the plt.hist( statements in the 1st plot section to see the effect)
    3. xdata (not np.log10(xdata)) to be plotted in the histogram
       • that 'workaround' with plotting np.log10(xdata) probably was the root cause for the misunderstanding in the comments

    Code:

    import numpy as np
    import matplotlib.pyplot as plt
    
    np.random.seed(42)  # just to have repeatable results for the answer
    
    xdata=np.random.normal(5e5,2e5,int(1e4))
    # MIN_xdata, MAX_xdata = np.min(xdata), np.max(xdata) 
    # print(f"{MIN_xdata}, {MAX_xdata}")  # note the negative values
    
    # cut off potential negative values (log function isn't defined for <= 0 )
    xdata = np.ma.masked_less_equal(xdata, 0)
    MIN_xdata, MAX_xdata = np.min(xdata), np.max(xdata)
    # print(f"{MIN_xdata}, {MAX_xdata}")
    
    # align the bins to fit a log scale
    bins = 100
    bins_log_aligned = np.logspace(np.log10(MIN_xdata), np.log10(MAX_xdata), bins)
    
    # 1st plot
    plt.hist(xdata, bins = bins_log_aligned)  # note: xdata (not np.log10(xdata) )
    # plt.hist(xdata, bins = 100)
    plt.xscale('log')
    plt.show()
    
    # 2nd plot
    plt.semilogy(xdata)
    plt.show()