Let G = (V,E) be a directed graph with no positive length cycles. Modifying Dijkstra algorithm as follow, with s the source:

1. Initialize d(s) = 0, d(v) = int_min for all v in V \ {s}.

2. In each iteration, choose a node u with maximum d(u).

3. Redefine the tentative distance as: if d(v) < d(u) c(uv) then d(v) := d(u) c(uv).

Is this a correct algorithm to find the length of the longest path in G starting from s ? If not, give a counter example. I have seen a similar answer to this question such as this one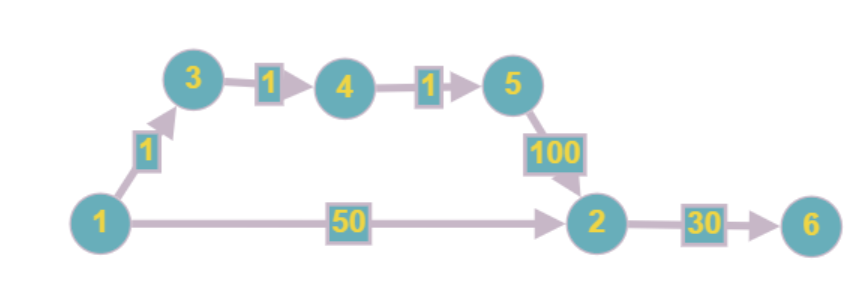

notice that you'll get into vertice 6 way before you'll get into vertice 5 so eventually the algorithm will won't repeat vertice 6 after it got into it as mention here:

When we are done considering all of the unvisited neighbors of the current node, mark the current node as visited and remove it from the unvisited set. A visited node will never be checked again (this is valid and optimal in connection with the behavior in step 6.

as you can see the idea beneath dijkstra is when you explore a node you won't need to explore never again and in the case of longest path is not true...