I am trying to write a recursive loop that prints all of the factorials from 1 to 14. I thought everything moved smoothly until I saw the output. What is my mistake?

double i,bounds = 14,factor = 1;

for(i = 0; i <= bounds; i  ){
    
    factor = factor * i;
    
    printf("%f          %f", i , factor);
    printf("\n");
    
}

return 0;

The result:

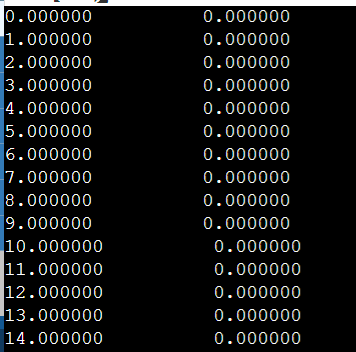
CodePudding user response：

Start your loop at i = 1 otherwise all factors will be 0 as observed. Your implementation is not a recursive loop, just an iterative loop.

#include <stdio.h>

int main() {
    double i = 0, bounds = 14, factor = 1;

    printf("%.0f! = %.0f\n", i, factor);
    for (i = 1; i <= bounds; i  ) {
        factor = factor * i;
        printf("%.0f! = %.0f\n", i, factor);
    }
    return 0;
}

Or with a single printf statement:

#include <stdio.h>

int main() {
    double i = 0, bounds = 14, factor = 1;

    for (;;) {
        printf("%.0f! = %.0f\n", i, factor);
        if (i >= bounds)
            break;
        i  = 1;
        factor = factor * i;
    }
    return 0;
}

CodePudding user response：

Writing recursive functions can be tricky.
That is why a problem like this is, as shown, easily solved with simple iterations.

However, since you asked: "what is my mistake?"
The posted code shows no sign of being a recursive function.
On the other hand, this does:

#include <stdio.h>

double factorial( int n ) {
    double f = 1.0;
    if( n > 1 )
        f = n * factorial( n - 1 ); // here's where Alice goes down the rabbit hole
    printf( "".0lf = -!\n", f, n ); // and here is where she returns
    return f;
}

int main() {
    factorial( 14 );

    return 0;
}

                     1 =  1!
                     2 =  2!
                     6 =  3!
                    24 =  4!
                   120 =  5!
                   720 =  6!
                  5040 =  7!
                 40320 =  8!
                362880 =  9!
               3628800 = 10!
              39916800 = 11!
             479001600 = 12!
            6227020800 = 13!
           87178291200 = 14!

You can extend this to a few higher values (double's have the capacity), but you will soon encounter errors where there are not enough bits to accurately represent the factorial. Plausible, but wrong, values will be printed.

EDIT
Once you've got the fundamentals working, you can begin to extend the code.

#include <stdio.h>

double factorial( int n ) {
    double f = 1.0;
    if( n > 1 ) f = n * factorial( n - 1 );
    printf( ".0lf = -! = ", f, n );
    char *pref = "";
    while( n )
        printf( "%s%d", pref, n-- ), pref = "x";
    puts( "" );
    return f;
}

int main() {
    factorial( 15 );

    return 0;
}

            1 =  1! = 1
            2 =  2! = 2x1
            6 =  3! = 3x2x1
           24 =  4! = 4x3x2x1
          120 =  5! = 5x4x3x2x1
          720 =  6! = 6x5x4x3x2x1
         5040 =  7! = 7x6x5x4x3x2x1
        40320 =  8! = 8x7x6x5x4x3x2x1
       362880 =  9! = 9x8x7x6x5x4x3x2x1
      3628800 = 10! = 10x9x8x7x6x5x4x3x2x1
     39916800 = 11! = 11x10x9x8x7x6x5x4x3x2x1
    479001600 = 12! = 12x11x10x9x8x7x6x5x4x3x2x1
   6227020800 = 13! = 13x12x11x10x9x8x7x6x5x4x3x2x1
  87178291200 = 14! = 14x13x12x11x10x9x8x7x6x5x4x3x2x1
1307674368000 = 15! = 15x14x13x12x11x10x9x8x7x6x5x4x3x2x1

(If you blur your eyes and look at that result, you begin to see "the rabbit hole". Odd to realise the 'bottom' of the recursion is the 'top' of that mound.)

EDIT2:
And, once things are in place, there's no end to the variations...

#include <stdio.h>

double factorial( int n ) {
    return ( n == 1 ) ? 1.0 : n * factorial( n - 1 );
}

int main() {
    for( int n = 16; n; n-- ) {
        printf( ".0lf = -! = ", factorial( n ), n );
        char *pref = "";
        for( int x = 1; x <= n; x   )
            printf( "%s%d", pref, x ), pref = "x";
        puts( "" );
    }

    return 0;
}

20922789888000 = 16! = 1x2x3x4x5x6x7x8x9x10x11x12x13x14x15x16
 1307674368000 = 15! = 1x2x3x4x5x6x7x8x9x10x11x12x13x14x15
   87178291200 = 14! = 1x2x3x4x5x6x7x8x9x10x11x12x13x14
    6227020800 = 13! = 1x2x3x4x5x6x7x8x9x10x11x12x13
     479001600 = 12! = 1x2x3x4x5x6x7x8x9x10x11x12
      39916800 = 11! = 1x2x3x4x5x6x7x8x9x10x11
       3628800 = 10! = 1x2x3x4x5x6x7x8x9x10
        362880 =  9! = 1x2x3x4x5x6x7x8x9
         40320 =  8! = 1x2x3x4x5x6x7x8
          5040 =  7! = 1x2x3x4x5x6x7
           720 =  6! = 1x2x3x4x5x6
           120 =  5! = 1x2x3x4x5
            24 =  4! = 1x2x3x4
             6 =  3! = 1x2x3
             2 =  2! = 1x2
             1 =  1! = 1

This last example is "wasteful" as it recalculates the result for diminishing values of 'n'. But, it's good to explore alternatives and variations. This last version could be "built into" a calculator program that, for a limited range of integers, simply calculates "n!", returning a single result for display.

The printing functionality could be condensed somewhat, too...

int main() {
    for( int n = 1; n <= 17; n   ) {
        printf( ".0lf = -! = ", factorial( n ), n );
        for( int x = 1; x <= n; x   )
            printf( "%d%c", x, "x\n"[x==n] );
    }
    return 0;
}