Fit Surface Plasmon Resonance (SPR) data in ggplot-CodePudding

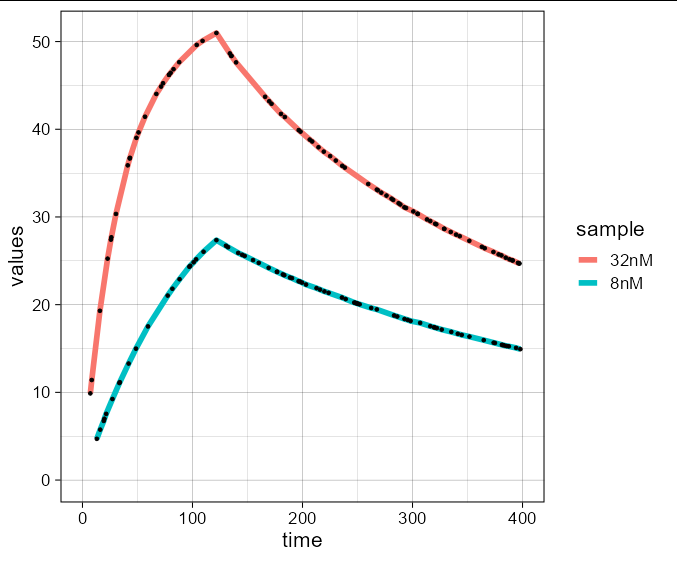
I am trying to fit association-dissociation SPR kinetics data for a protein and small molecule for two concentrations using ggplot2. The data is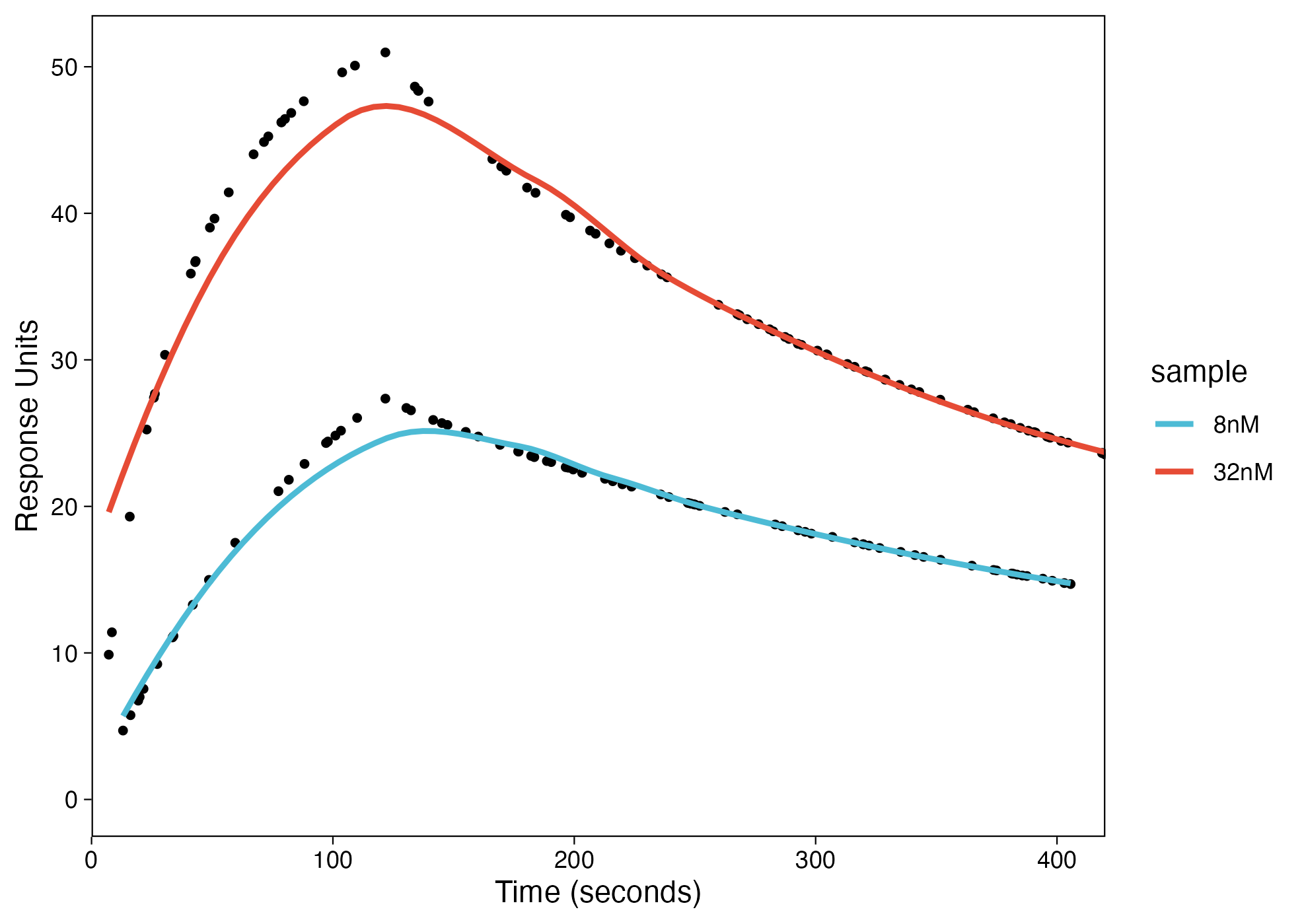

As you can see that the fit did not work using method = "loess". I need something like this(there are 5 concentrations here):

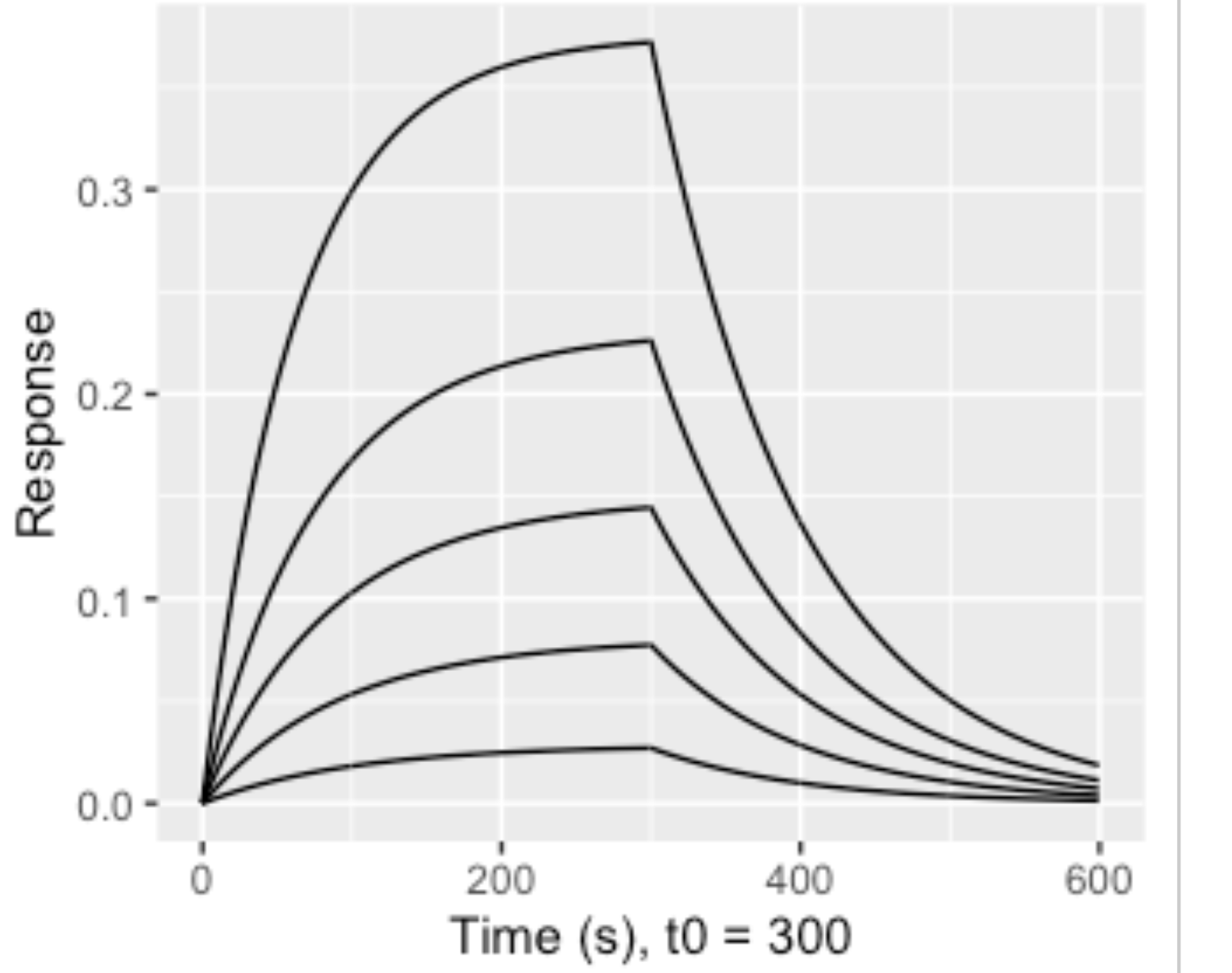
The fitting requires 1:1 Langmuir model but I am not sure how I can do that in ggplot. Can someone please help me?

Here is the equation:

This is from the

Edit

It is possible to fit the results to the data using non-linear least squares, employing the binding1to1 function from pbm, but it requires a bit of method tweaking to get the model to fit. It would probably be better to create a model then plot the predictions rather than using geom_smooth. However, if you really wanted to, you could do:

df %>%
  ggplot(aes(time, values, color = sample))  
  geom_smooth(method = nls, se = FALSE, n = 1000,
              formula = y ~ binding1to1(x, 123, 32e-9, kon, koff, rmax),
              method.args = list(
                start = list(kon = 2000, koff = 0.02, rmax = 2e4),
                control = nls.control(minFactor = 1e-6, maxiter = 1000)
              ),
   data =  df[df$time > 0 & df$sample == "32nM",])  
  geom_smooth(method = nls, se = FALSE, n = 1000,
              formula = y ~ binding1to1(x, 123, 8e-9, kon, koff, rmax),
              method.args = list(
                start = list(kon = 3000, koff = 0.02, rmax = 2e4),
                control = nls.control(minFactor = 1e-9, maxiter = 10000)
              ),
              data =  df[df$time > 0 & df$sample == "8nM",])  
  geom_point(color = 'black', size = 1)  
  theme_linedraw(base_size = 16)  
  xlim(c(0, 400))

If you want to actually fit a model from which to extract the parameters and plot, you can do:

library(tidyverse)
library(pbm)

df <- read.csv("SPR.csv") %>%
  filter(time >= 0) %>%
  mutate(sample = as.numeric(gsub("\\D ", "", sample)) * 1e-9,
         values = values * 1e-3) %>%
  group_by(sample) %>%
  mutate(tmax = time[which.max(values)])

fit_fun <- function(time, tmax, sample, kon, koff, rmax) {
  unlist(Map(function(time, tmax, sample) {
    binding1to1(time, tmax, sample, kon, koff, rmax)
    }, time, tmax, sample))
}

mod <- nls(values ~ fit_fun(time, tmax, sample, kon, koff, rmax),
    data = df,
    start = list(kon = 3000, koff = 0.02, rmax = 2),
    control = nls.control(minFactor = 1e-9, maxiter = 10000))

This gives us a model with the best fitting values for the various parameters:

mod
#> Nonlinear regression model
#>   model: values ~ fit_fun(time, tmax, sample, kon, koff, rmax)
#>    data: df
#>       kon      koff      rmax 
#> 8.925e 05 2.521e-03 5.445e-02 
#>  residual sum-of-squares: 5.219e-05
#> 
#> Number of iterations to convergence: 536 
#> Achieved convergence tolerance: 5.155e-07

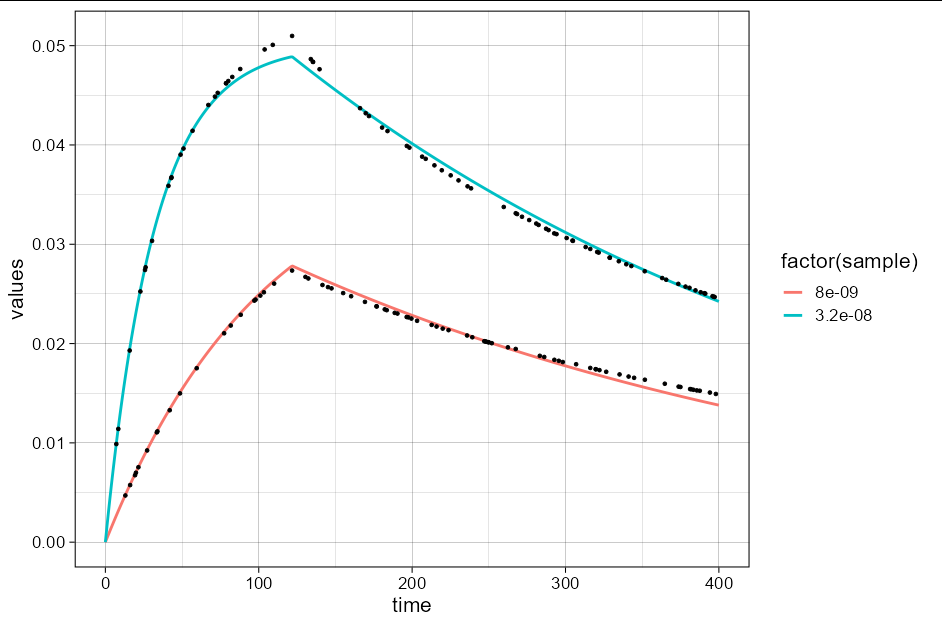
We can then predict the output of the model over the range of our input variables:

pred_df <- expand.grid(time = 0:400, sample = c(8, 32) * 1e-9, 
                       tmax = df$tmax[1])

pred_df$values <- predict(mod, pred_df)

And we can plot it like this:

df %>%
  ggplot(aes(time, values, color = factor(sample)))  
  geom_line(data = pred_df, size = 1)  
  geom_point(color = 'black', size = 1)  
  theme_linedraw(base_size = 16)  
  xlim(c(0, 400))