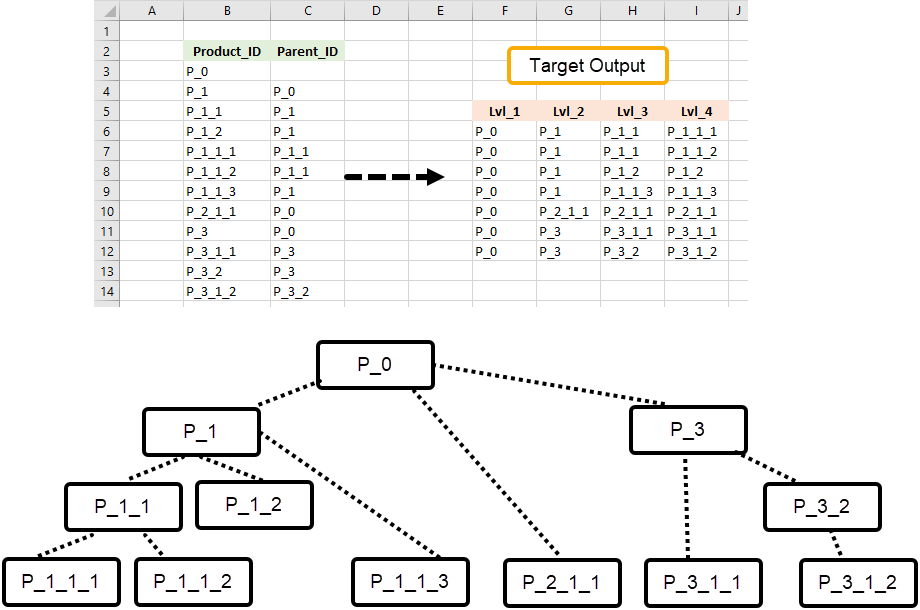
I need to flatten a hierarchy in Oracle 12c, the sample simplified input is on the left with an added graphical representation at the bottom (screenshot below). The target output is highlighted on the right side.
There are 4 levels where Lvl_1 is the top of the hierarchy and there are missing levels. The requirement is that the missing levels should be filled with the lowest level of detail available. There are multiple samples like P_1_2
I'm not sure how to tackle the problem, I have found several solutions for SQL Server not Oracle and none of them manages the missing levels criteria as this requirement
Anyone who have done something like this?
CREATE TABLE ztest_product
(
PRODUCT_ID VARCHAR(10)
, PARENT_ID VARCHAR(10)
)
;
Insert into ztest_product(PRODUCT_ID, PARENT_ID) values ('P_0', NULL);
Insert into ztest_product(PRODUCT_ID, PARENT_ID) values ('P_1', 'P_0');
Insert into ztest_product(PRODUCT_ID, PARENT_ID) values ('P_1_1', 'P_1');
Insert into ztest_product(PRODUCT_ID, PARENT_ID) values ('P_1_2', 'P_1');
Insert into ztest_product(PRODUCT_ID, PARENT_ID) values ('P_1_1_1', 'P_1_1');
Insert into ztest_product(PRODUCT_ID, PARENT_ID) values ('P_1_1_2', 'P_1_1');
Insert into ztest_product(PRODUCT_ID, PARENT_ID) values ('P_1_1_3', 'P_1');
Insert into ztest_product(PRODUCT_ID, PARENT_ID) values ('P_2_1_1', 'P_0');
Insert into ztest_product(PRODUCT_ID, PARENT_ID) values ('P_3', 'P_0');
Insert into ztest_product(PRODUCT_ID, PARENT_ID) values ('P_3_1_1', 'P_3');
Insert into ztest_product(PRODUCT_ID, PARENT_ID) values ('P_3_2', 'P_3');
Insert into ztest_product(PRODUCT_ID, PARENT_ID) values ('P_3_1_2', 'P_3_2');
COMMIT;
CodePudding user response:
You can find the leaf nodes of the hierarchy and use SYS_CONNECT_BY_PATH to find the path taken and then split it into different levels:
SELECT lvl_1,
COALESCE(lvl_2, lvl_1) AS lvl_2,
COALESCE(lvl_3, lvl_2, lvl_1) AS lvl_3,
COALESCE(lvl_4, lvl_3, lvl_2, lvl_1) AS lvl_4
FROM (
SELECT REGEXP_SUBSTR(
SYS_CONNECT_BY_PATH(product_id, ','), ',([^,] )', 1, 1, NULL, 1
) AS lvl_1,
REGEXP_SUBSTR(
SYS_CONNECT_BY_PATH(product_id, ','), ',([^,] )', 1, 2, NULL, 1
) AS lvl_2,
REGEXP_SUBSTR(
SYS_CONNECT_BY_PATH(product_id, ','), ',([^,] )', 1, 3, NULL, 1
) AS lvl_3,
REGEXP_SUBSTR(
SYS_CONNECT_BY_PATH(product_id, ','), ',([^,] )', 1, 4, NULL, 1
) AS lvl_4
FROM ztest_product
WHERE CONNECT_BY_ISLEAF = 1
START WITH parent_id IS NULL
CONNECT BY PRIOR product_id = parent_id
)
Which, for your sample data, outputs:
| LVL_1 | LVL_2 | LVL_3 | LVL_4 |
|---|---|---|---|
| P_0 | P_1 | P_1_1 | P_1_1_1 |
| P_0 | P_1 | P_1_1 | P_1_1_2 |
| P_0 | P_1 | P_1_1_3 | P_1_1_3 |
| P_0 | P_1 | P_1_2 | P_1_2 |
| P_0 | P_2_1_1 | P_2_1_1 | P_2_1_1 |
| P_0 | P_3 | P_3_1_1 | P_3_1_1 |
| P_0 | P_3 | P_3_2 | P_3_1_2 |
CodePudding user response:
Here is a preparation query that generates the missing nodes without playing with regexp_substr which may lead to performance problem if your data set is big:
WITH cnodes AS (
SELECT LEVEL AS lvl, p.*, connect_by_isleaf AS is_leaf FROM ztest_product p
START WITH product_id IN (
SELECT product_id FROM ztest_product WHERE parent_id IS NULL
)
CONNECT BY PRIOR product_id = parent_id
),
inodes AS (
SELECT cn.* FROM cnodes cn
WHERE NOT EXISTS(
SELECT 1 FROM cnodes c1 WHERE cn.product_id = c1.parent_id AND cn.lvl = c1.lvl 1 AND cn.lvl < 4
)
AND is_leaf = 1 AND lvl < 4
)
SELECT * FROM (
SELECT lvl, product_id, parent_id FROM (
SELECT lvl LEVEL AS lvl, product_id, product_id AS parent_id FROM inodes
CONNECT BY LEVEL < 5 - lvl AND PRIOR product_id = product_id AND PRIOR sys_guid() IS NOT NULL
UNION ALL
SELECT lvl, product_id, parent_id FROM cnodes
)
)
ORDER BY lvl, parent_id, product_id
;
Result is the completed tree with the missing nodes, where the added nodes are parent of themselves:
1 P_0
2 P_1 P_0
2 P_2_1_1 P_0
2 P_3 P_0
3 P_1_1 P_1
3 P_1_1_3 P_1
3 P_1_2 P_1
3 P_2_1_1 P_2_1_1
3 P_3_1_1 P_3
3 P_3_2 P_3
4 P_1_1_1 P_1_1
4 P_1_1_2 P_1_1
4 P_1_1_3 P_1_1_3
4 P_1_2 P_1_2
4 P_2_1_1 P_2_1_1
4 P_3_1_1 P_3_1_1
4 P_3_1_2 P_3_2