Calculate lethal dosis concentration calculation (LD50) on R-CodePudding

I am trying to calculate LD50 (lethal doses concentration that kills 50% of the organisms) for bees at diferent exposure concentrations (0, 3, 30 and 300ng) of a pesticide. I mesure supervivency every 4 hours.

Data:

Control<-c(100, 100, 100,  96, 96,  96,  96,  72,  60,  60,  60,  60, 60,  52,  48,  48, 40,  40)
"300ng" <- c(100.00, 100.00, 100.00,  96.30,  96.30,  92.59,  92.59,70.37, 62.96,  44.44,  40.74,  37.04, 29.63,  25.93,  25.93,22.22,  11.11,  11.11)
"30ng" <- c(100.00,  96.30,  96.30,  96.30,  96.30,  96.30,  96.30,  85.19,  81.48,  77.78,  74.07,  74.07,  74.07,  70.37,  70.37,  70.37,  70.37,  62.96)
"3ng" <- c(100.00, 100.00, 100.00, 100.00, 100.00,  96.30,  85.19,  74.07,  70.37,  66.67,  66.67,  66.67,  66.67,  59.26,  59.26,  59.26,  59.26,  55.56)
HoursExp <- c(0,  4,  8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68)

Viewing data

plot(`300ng`~HoursExp, type="l", col=1)
points(`30ng`~HoursExp, type="l", col=2)
points(`3ng`~HoursExp, type="l", col=3)
points(Control~HoursExp, type="l", col=4)

I`d like to try with Trimmed Spearman-Karber Method tsk function

install.packages("tsk", repos="http://R-Forge.R-project.org")
require(tsk)
require(drc)

The problem is that i cant understand how to use that function in order to obtain the LD50 at 24 and 48 hours of exposition with confidence intervals. Other method is also good for me, but i can`t find any for my purpuses.

CodePudding user response：

The {drc} package has the functionality you are looking for. However your dataset is too limited to be able to calculate any confidence interval on the model parameters. Essentially you need your curve to plateau at the bottom so the model can converge on a confidence interval for the fit. The method below will work if you have a more complete dataset in the future though.

Since you included a control value at each time point that seems to change substantially, I calculated a relative_survival by normalizing to this value to help standardize the top of the curves. Also, I constrained some of the fit parameters based on basic understanding of what the LD50 should be, the curve should start around 1, eventually reach 0 and the slope should be negative.

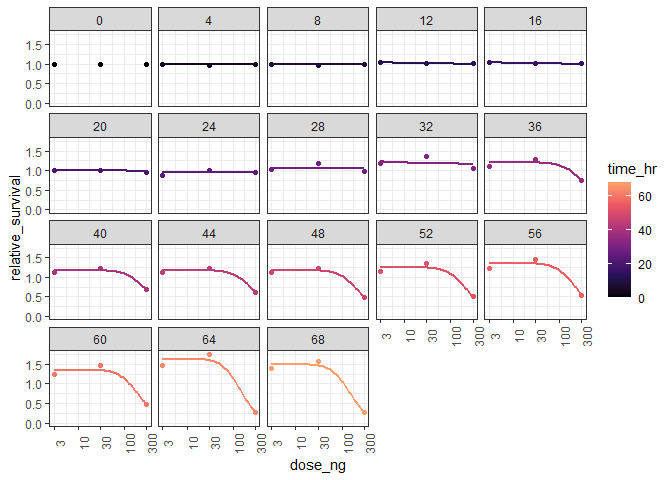
I started with a quick visualization of the whole dataset to help set expectations about what kind of modeling should be possible with this data.

Note for some reason in the {drc} package the sign of the Hill slope is reversed. So for decreasing curves the value is reported as positive.

library(tidyverse)
library(drc)

# set up data
d <- tibble(
control = c(100, 100, 100,  96, 96,  96,  96,  72,  60,  60,  60,  60, 60,  52,  48,  48, 40,  40),
ng_300 = c(100.00, 100.00, 100.00,  96.30,  96.30,  92.59,  92.59,70.37, 62.96,  44.44,  40.74,  37.04, 29.63,  25.93,  25.93,22.22,  11.11,  11.11),
ng_30 = c(100.00,  96.30,  96.30,  96.30,  96.30,  96.30,  96.30,  85.19,  81.48,  77.78,  74.07,  74.07,  74.07,  70.37,  70.37,  70.37,  70.37,  62.96),
ng_3 = c(100.00, 100.00, 100.00, 100.00, 100.00,  96.30,  85.19,  74.07,  70.37,  66.67,  66.67,  66.67,  66.67,  59.26,  59.26,  59.26,  59.26,  55.56),
time_hr = c(0,  4,  8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68))

# reformat data to facilitate analysis
e <- d %>% 
  pivot_longer(starts_with("ng"), names_prefix = "ng_", names_to = "dose_ng", values_to = "survival") %>% 
  mutate(relative_survival = survival/control,
         dose_ng = as.numeric(dose_ng))

# visualize to understand dose-response trend over time
e %>% 
  ggplot(aes(dose_ng, relative_survival, color = time_hr))  
  geom_point()  
  stat_smooth(method = "drm",
              method.args = list(fct = LL.4(names = c("hill", "bottom", "top", "EC50")),
                                 type = "continuous",
                                   upperl = c(10, 0.1, Inf, Inf),
                                   lowerl = c(0.1, -0.1, -Inf, -Inf)
                                   ),
              se = F)  
  scale_x_log10()  
  ylim(0, NA)  
  facet_wrap(~time_hr)  
  scale_color_viridis_c(option = "A", end = 0.8)  
  theme_bw()  
  theme(axis.text.x = element_text(angle = 90))


# build model
drc_mod <- e %>% 
  filter(time_hr %in% c(24, 48)) %>% 
  mutate(time_hr = factor(time_hr)) %>% 
  drm(
    formula = relative_survival ~ dose_ng,
    curveid = time_hr,
    data = .,
    fct = LL.4(names = c("hill", "bottom", "top", "EC50")),
    type = "continuous",
    upperl = c(10, 0.1, Inf, Inf),
    lowerl = c(0.1, -0.1, -Inf, -Inf)
  )

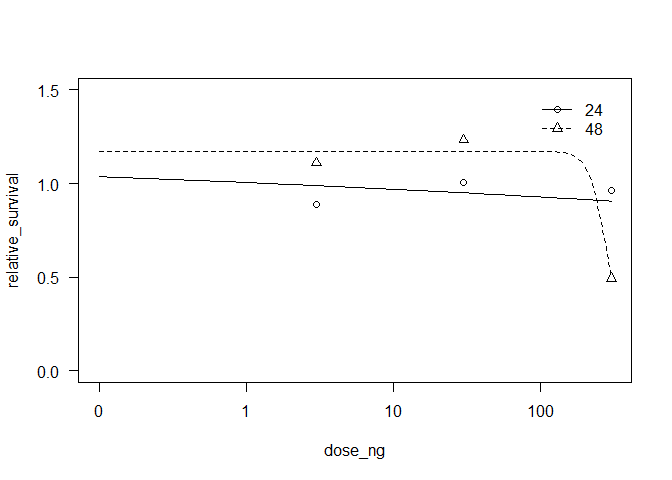
# visualize model
plot(drc_mod, ylim = c(0, 1.5), xlim = c(0, 300))


# report coefficients for each time point
drc_mod$coefficients
#>      hill:24      hill:48    bottom:24    bottom:48       top:24       top:48 
#> 1.000000e-01 7.418135e 00 2.000000e-01 8.080277e-02 1.184212e 00 1.172833e 00 
#>      EC50:24      EC50:48 
#> 3.490536e 06 2.805554e 02

# assess confidence interval on each model parameter
drc_mod %>% confint()
#>           2.5 % 97.5 %
#> hill:24     NaN    NaN
#> hill:48     NaN    NaN
#> bottom:24   NaN    NaN
#> bottom:48   NaN    NaN
#> top:24      NaN    NaN
#> top:48      NaN    NaN
#> EC50:24     NaN    NaN
#> EC50:48     NaN    NaN

^{Created on 2022-10-21 by the reprex package (v2.0.1)}