How to fit a straight line to part of a curve-CodePudding

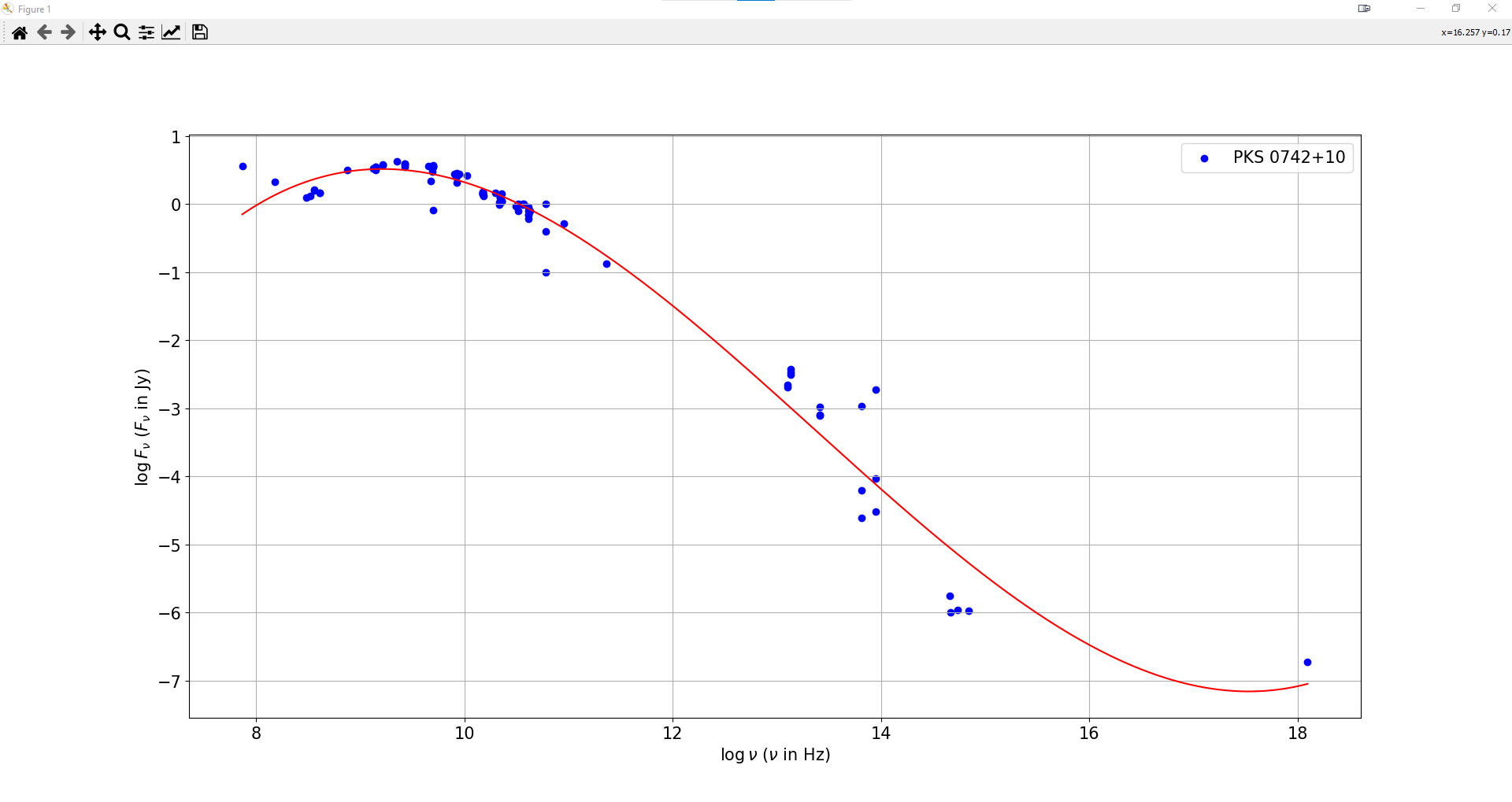
I have a set of data from a pd.DataFrame which looks like this, with a 3rd-order polynomial fitted to it:

which is fit by

# Find the 3rd-order polynomial which fits the SED
coefs = poly.polyfit(x, y, 3) # find the coeffs
x_new = np.linspace(lower, upper, num=len(x)*10) # space to plot the fit
ffit = poly.Polynomial(coefs) # find the polynomial

How could I find the straight line that fits only part of the data, for example, just the downward slope within 9.5 < x < 15 ?

I could slice the dataframe into pieces with

left = pks[pks[xvar] < nu_to]
right = pks[pks[xvar] > nu_to]

but I'd like to avoid that, since I'll have to do the same thing with many datasets.

This question is about MatLab This current question is a distillation of my previous one.

CodePudding user response：

Assuming the curve shape is always going to be similar to the example, you could fit a line to the portion of your dataset limited by the ymax and ymin values. You could automate the detection of that subset by calculating the y range between the ymax and ymin values, as well as the corresponding x values. The use of the min and max inside the slice is to take into account the min and max values of y might not always be in the same order:

linearx = x[min(np.argmax(y), np.argmin(y)): max(np.argmax(y), np.argmin(y)) 1]
lineary = y[min(np.argmax(y), np.argmin(y)): max(np.argmax(y), np.argmin(y)) 1]

CodePudding user response：

Maybe you just use the linear part of your polynomial fit. The idea is to get slope and offset by first eliminating the quadratic term. Say you have

y = a x^3 b x^2 c x d,

setting x -> x - b / 3a removes the quadratic term. The remaining function has a linear slope of

c' = c - b^2 / 3a

and an offset of

d'= d-b c / 3a 2b^3 / 27a^2.

Transforming the linear part back gives you the final offset

d'' = d - b^3/ 27a^2

so the linear part is given by

y = ( c - b^2 / 3a ) x d - b^3/ 27a^2