cartopy: Why isn't my circle moving along the great circle path?-CodePudding

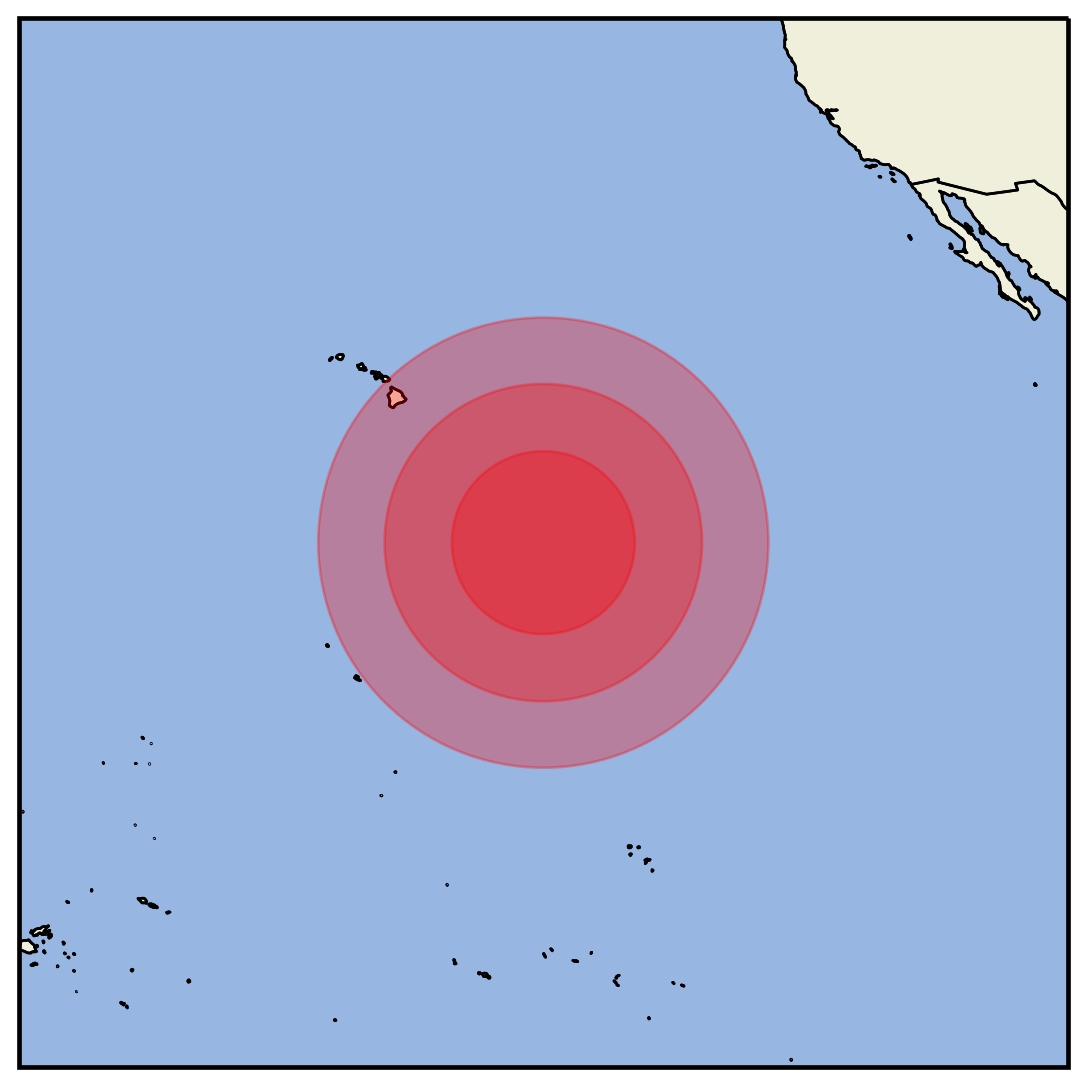
I'm having trouble using cartopy ...

I have some locations (mainly changing in lat) and I want to draw some circles along the this great circle path. Here's the code

import cartopy.crs as ccrs
import cartopy.feature as cfeature
import cartopy
import numpy as np

import matplotlib.pyplot as plt
import matplotlib.patches as mpatches

points = np.array([[-145.624, 14.8853],
[-145.636, 10.6289],
[-145.647, 6.3713]])

proj2      = ccrs.Orthographic(central_longitude= points[1,0], central_latitude=  points[1,1]) # Spherical map
pad_radius = compute_radius(proj2, points[1,0],points[1,1], 35)

resolution = '50m'

fig = plt.figure(figsize=(112,6), dpi=96)
ax = fig.add_subplot(1, 1, 1, projection=proj2)
ax.set_xlim([-pad_radius, pad_radius])
ax.set_ylim([-pad_radius, pad_radius])

ax.imshow(np.tile(np.array([[cfeature.COLORS['water'] * 255]], dtype=np.uint8), [2, 2, 1]), origin='upper', transform=ccrs.PlateCarree(), extent=[-180, 180, -180, 180])

ax.add_feature(cfeature.NaturalEarthFeature('physical', 'land', resolution, edgecolor='black', facecolor=cfeature.COLORS['land']))
ax.add_feature(cfeature.NaturalEarthFeature('cultural', 'admin_0_countries', resolution, edgecolor='black', facecolor='none'))

# Loop over the points
# Compute the projected circle at that point
# Plot it!
for i in range(len(points)):
    thePt = points[i,0], points[i,1]
    r_or = compute_radius(proj2, points[i,0], points[i,1],  10)
    print(thePt, r_or)
    c= mpatches.Circle(xy=thePt, radius=r_or, color='red', alpha=0.3, transform=proj2, zorder=30)
    # print(c.contains_point(points[i,0], points[i,1]))
    ax.add_patch(c)
fig.tight_layout()
plt.show()

Compute radius is:

def compute_radius(ortho, lon, lat, radius_degrees):
    '''
    Compute a earth central angle around lat, lon
    Return phi in terms of projection desired
    This only seems to work for non-PlateCaree projections
    '''
    phi1 = lat   radius_degrees if lat <= 0 else lat - radius_degrees
    _, y1 = ortho.transform_point(lon, phi1, ccrs.PlateCarree()) # From lon/lat in PlateCaree to ortho
    return abs(y1)

And what I get for output:

(-145.624, 14.8853) 638304.2929446043 (-145.636, 10.6289) 1107551.8669600221 (-145.647, 6.3713) 1570819.3871025692

You can see the interpolated points going down in lat (lon is almost constant), but the radius is growing smaller with lat and the location isn't changing at all???

CodePudding user response：

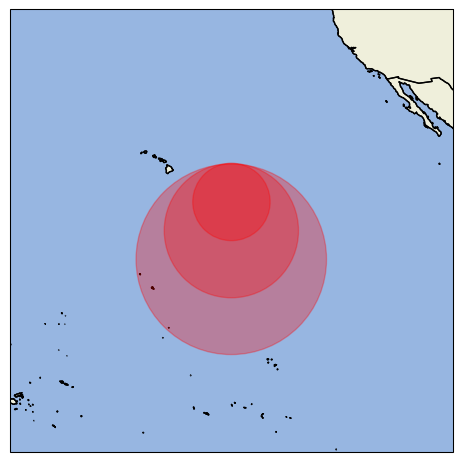
Thanks for rewriting the example, that clears things up!

I think the key point is that you need to convert the x/y coordinates that you use for the Circle as well, or vice versa keep the radius also in lat/lon (probably close but not identical). Now you mix and match, where the radius is based on the Orthographic projection, but the x/y are lat/lon. Because of that, the points do move along the path you want, but it's just incredibly close to the origin of the plot due to the incorrect units.

Something like this might help you along:

points = np.array([
    [-145.624, 14.8853],
    [-145.636, 10.6289],
    [-145.647, 6.3713]],
)

proj2      = ccrs.Orthographic(
    central_longitude= points[1,0], 
    central_latitude=  points[1,1],
)
pad_radius = compute_radius(proj2, points[1,0],points[1,1], 35)

resolution = '50m'

fig, ax = plt.subplots(
    figsize=(12,6), dpi=96, subplot_kw=dict(projection=map_proj, facecolor=cfeature.COLORS['water']),
)

ax.add_feature(cfeature.NaturalEarthFeature('physical', 'land', resolution, edgecolor='black', facecolor=cfeature.COLORS['land']))
ax.add_feature(cfeature.NaturalEarthFeature('cultural', 'admin_0_countries', resolution, edgecolor='black', facecolor='none'))

ax.set_extent((-pad_radius, pad_radius, -pad_radius, pad_radius), crs=proj2)

for lon, lat in points:
    r_or = compute_radius(proj2, lon, lat,  10)

    ### I think this is what you intended!
    mapx, mapy = proj2.transform_point(lon, lat, ccrs.PlateCarree())
    ###

    c= mpatches.Circle(xy=(mapx, mapy), radius=r_or, color='red', alpha=0.3, transform=proj2, zorder=30)
    ax.add_patch(c)

CodePudding user response：

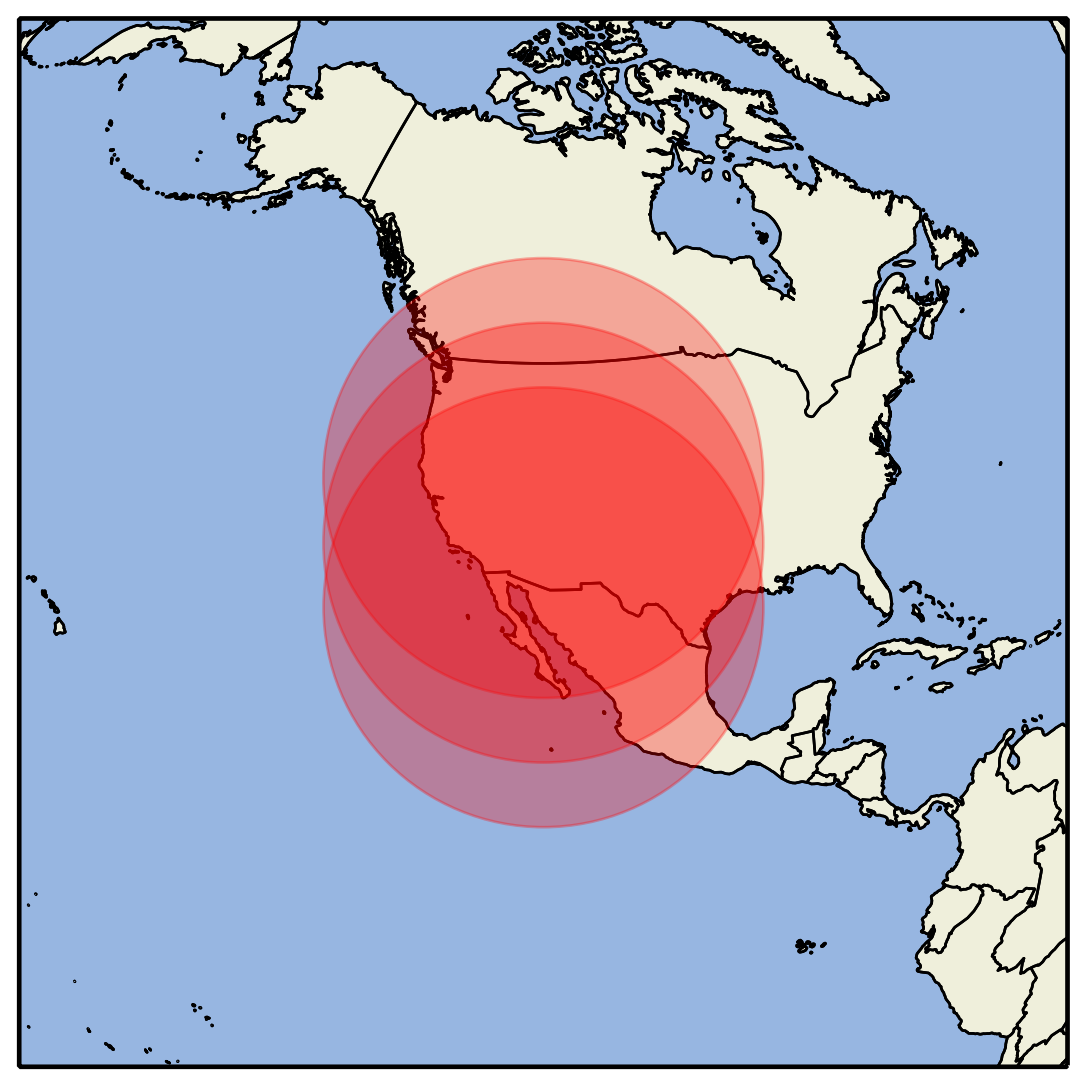
Here's the complete answer. I was not converting the lat/lon into the orthographic projection coords... and apparently it wants the size of the circle to be in meters -- hence I use a function to change degrees (which I know for my circle) into meters:

def deg2m(val_degree):
    """
    Compute surface distance in meters for a given angular value in degrees
    Uses the definition of a degree on the equator... 
    """
    geod84 = Geod(ellps='WGS84')
    lat0, lon0 = 0, 90
    _, _, dist_m = geod84.inv(lon0, lat0,  lon0 val_degree, lat0)
    return dist_m


# Data points where I wish to draw circles
points = np.array([[-111.624, 30.0],
[-111.636, 35.0],
[-111.647, 40.0]])

proj2      = ccrs.Orthographic(central_longitude= points[1,0], central_latitude=  points[1,1]) # Spherical map
pad_radius = compute_radius(proj2, points[1,0],points[1,1], 45) # Generate a region bigger than our circles

resolution = '50m'

fig = plt.figure(figsize=(112,6), dpi=96)
ax = fig.add_subplot(1, 1, 1, projection=proj2)
# Bound our plot/map
ax.set_xlim([-pad_radius, pad_radius])
ax.set_ylim([-pad_radius, pad_radius])

ax.imshow(np.tile(np.array([[cfeature.COLORS['water'] * 255]], dtype=np.uint8), [2, 2, 1]), origin='upper', transform=ccrs.PlateCarree(), extent=[-180, 180, -180, 180])
ax.add_feature(cfeature.NaturalEarthFeature('physical', 'land', resolution, edgecolor='black', facecolor=cfeature.COLORS['land']))
ax.add_feature(cfeature.NaturalEarthFeature('cultural', 'admin_0_countries', resolution, edgecolor='black', facecolor='none'))

r_or = deg2m(17) # Compute the size of circle with a radius of 17 deg

# Loop over the points
# Compute the projected circle at that point
# Plot it!
for i in range(len(points)):
    thePt = points[i,0], points[i,1]
    # Goes from lat/lon to coordinates in our Orthographic projection
    mapx, mapy = proj2.transform_point(points[i,0], points[i,1], ccrs.PlateCarree())
    c= mpatches.Circle(xy=(mapx, mapy), radius=r_or, color='red', alpha=0.3, transform=proj2, zorder=30)
    ax.add_patch(c)
fig.tight_layout()
plt.show()

I've verified that the deg2m routine works since it's about 17 deg of lat from Phoenix AZ to the Canadian border (approx) which is nearby these test points.