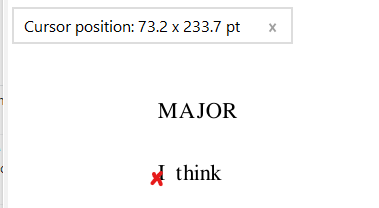
The PDF content below renders with the correct vertical positions, but how?
1 0 0 -1 0 792 cm
q
.75 0 0 .75 72 192.75 cm
BT
/F4 14.666667 Tf
1 0 0 -1 0 .80265617 Tm
0 -13.2773438 Td <0030> Tj
12.2087708 0 Td <0024> Tj
8.6870575 0 Td <003C> Tj
9.7756042 0 Td <0032> Tj
11.4001007 0 Td <0035> Tj
ET
Q
q
.75 0 0 .75 72 222.75 cm
BT
/F4 14.666667 Tf
1 0 0 -1 4.0719757 .80265617 Tm
0 -13.2773438 Td <002C> Tj
4.0719757 0 Td <0003> Tj
4.0719757 0 Td <0057> Tj
4.0719757 0 Td <004B> Tj
8.1511078 0 Td <004C> Tj
3.2561493 0 Td <0051> Tj
8.1511078 0 Td <004E> Tj
ET
Q
Renders correctly:
MAJOR
I think
However I can't understand how the y positions are calculated to do this (x is fine). The Text Rendering Matrix (TRM) is given by Text Matrix (TM) multiplied by Current Transformation Matrix (CTM) PDF1.7 Reference section 9.4.4. CTM is the identity matrix multiplied by each "cm" operation.
So for the first snippet,
CTM = [1 0 0 -1 0 792] x [0.75 0 0 0.75 72 192.75] = [0.75 0 0 -0.75 72 786.75]
TRM is TM x CTM:
TRM = [1 0 0 -1 0 0.8026] x [0.75 0 0 -0.75 72 786.75] = [0.75 0 0 0.75 72 786.1]
So, ignoring small details, the text will be rendered around y = 786 (actually 776 I reckon)
For the second snippet,
CTM = [1 0 0 -1 0 792] x [0.75 0 0 0.75 72 222.75] = [0.75 0 0 -0.75 72 816.75]
TRM = [1 0 0 -1 4.072 0.802] x [0.75 0 0 -0.75 72 816.75] = [0.75 0 0 0.75 75.05 816.4]
Again, ignoring small details, the text will be rendered around y = 816 (actually 806 I reckon)
But the y origin is the bottom of the page, and 816 is greater than 786. So how come the second snippet of text renders correctly below the first? I'm clearly missing something in the calculations, but I can't see what. Any ideas?
CodePudding user response:
Without going deep into matrices (not my forte, there is a slight error in my initial maths so images new corrected) you are working downwards from top left based on an inverted start point of 0 792 cm (Top Left corner)
The start of that snippet is above MAJOR 72 192.75 cm

Without outher transformations the text would be "UpsideDown" with M facing towards the bottom then the second 1 0 0 -1 mirrors it back upright and 0.8 "raises" it towards bottom so baseline is 193.5 ish from topleft at which point you "add" 0 -13.2773438 Td so the baseline is now about 205 from top left
Likewise, the origin for the second row is 72 222.75 cm down from above datum.
In both cases you placed their mirrored baseline even lower at 0 -13.2773438 Td thus both lines will be lower than shown above. In part due to the matrix inversions.
so here the second baseline is now at about 72 234 cm down from top left as subject to similar maths is roughly 222.75 .802 13.277 down but scale can also have effect.
Generally its best to use real time viewer of alterations (however this is not the best way just an example that by playing with rounded values I can see the effects).
CodePudding user response:
The error in your calculations is that you apply the cm matrix by multiplication from the right side. You instead have to apply it from the left side.
I.e. for the first snippet you have
CTM = [0.75 0 0 0.75 72 192.75] × [1 0 0 -1 0 792] = [0.75 0 0 -0.75 72 599.25]
and for the second snippet
CTM = [0.75 0 0 0.75 72 222.75] × [1 0 0 -1 0 792] = [0.75 0 0 -0.75 72 569.25]
With these current transformation matrices the rendered result is to be expected.
If you wonder how you should have known that you need to multiply from the left side...
This result is true in general for PDF: when a sequence of transformations is carried out, the matrix representing the combined transformation (M′) is calculated by premultiplying the matrix representing the additional transformation (MT) with the one representing all previously existing transformations (M):