Creating Stacked Density Plot with Weightings-CodePudding

I am attempting to use ggplot2 to create a weighted density plot showing the distribution of two groups that each account for a fraction of a certain distribution. The difficulty that I am encountering stems from the fact that although both groups have the same number of observations in the data, they have different weightings, and I would like for each group's area in the graph to reflect this difference in weightings.

My data look something like this.

var <- sort(rnorm(1000, mean = 5, sd = 2))
df <- tibble(id = c(rep(1, 1000), rep(2, 1000)), 
       var = c(var,var), 
       weight = c(rep(.1, 500), rep(.2, 500), rep(.9, 500), rep(.8, 500)))

Observe that, group 1 is given low weightings (.1 or .2) while group 2 is given high weighting of (.9 or .8). Also observe that for any given value of var has weightings that add up to 1. In the real data, the shares accounted for by each group differ in a more complex manner across the distribution of var.

I have tried plotting this data as follows, and although using weight captures the way that the distributions vary within each group, it does not capture the way that the distribution varies between groups.

library(ggplot2)

var <- rnorm(1000, mean = 5, sd = 2)

df %>%
  ggplot(aes(x = var, group = id, fill = factor(id), weight = weight))   
  geom_density(position = 'stack')

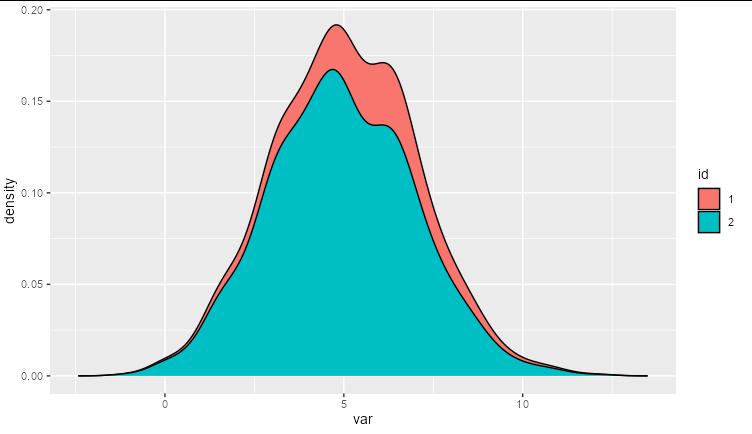
The resulting plot looks something like this.

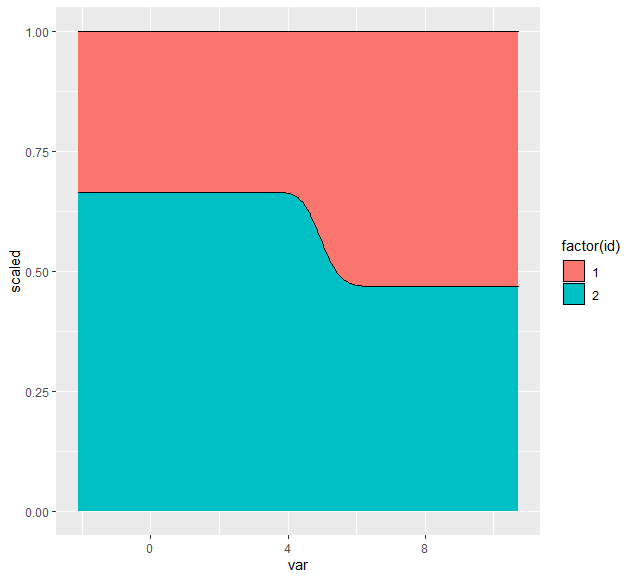
It is clear that the groups do not account for around 15% and 85% of the area under the density curve respectively, but the issue is clearer to see when we use position = 'fill'.

Each group seems to take up a similar area, apparently because the weighting is applied before grouping is accounted for. I would like to see a solution that results in the area associated with group 1 being commensurate with it's weight (i.e. much smaller than the area associated with group 2).

To clarify, it is the height associated with each group that should differ. In the above plot, the line of demarcation between group 1 and group 2 should be significantly higher, making the area taken up by group 1 significantly smaller.

CodePudding user response：

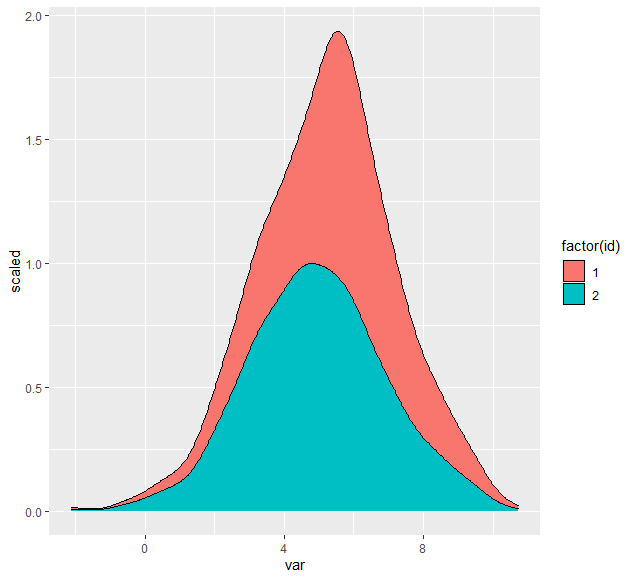
Dealing with the relative density of the two groups is a bit ambiguous. Clearly, each group's density needs to have an integral of 1 for it to be a true density. The closest you can come is probably to have the integral of both curves sum to 1, which I think requires you to do the density calculation yourself then plot as a stacked geom_area:

library(tidyverse)

df %>%
  nest(data = -id) %>%
  summarize(id = factor(id),
            weight = unlist(map(data, ~sum(.x$weight))),
            dens = map(data, function(.x) {
              x <- density(.x$var, weights = .x$weight/sum(.x$weight))
              data.frame(x = x$x, y = x$y)
              })) %>%
  mutate(weight = weight / sum(weight)) %>%
  unnest(dens) %>%
  mutate(y = y * weight) %>%
  ggplot(aes(x, y, fill = id))  
  geom_area(position = 'stack', color = 'black')  
  labs(y = 'density', x = 'var')

CodePudding user response：

I am not completely sure if I understand you correctly, but maybe you can calculate the value beforehand based on the weight and then stack it like this:

library(ggplot2)
library(dplyr)

# Stacked
df %>%
  mutate(weighted_var = var*weight) %>%
  ggplot(aes(x = weighted_var, fill = factor(id), group = id))  
  geom_density(position = 'stack')

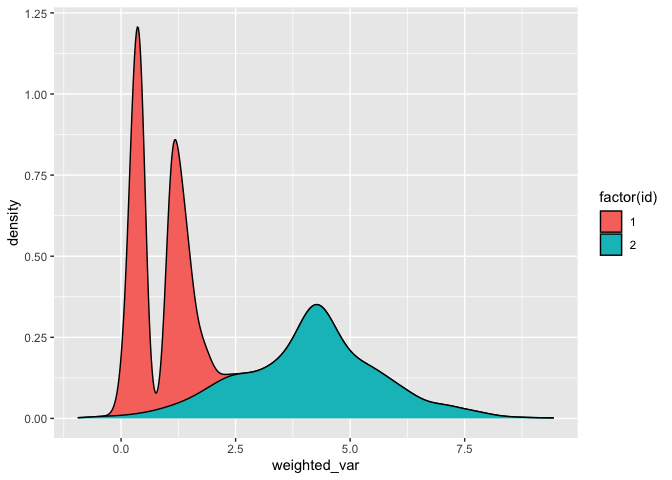
And check the groups with fill like this:

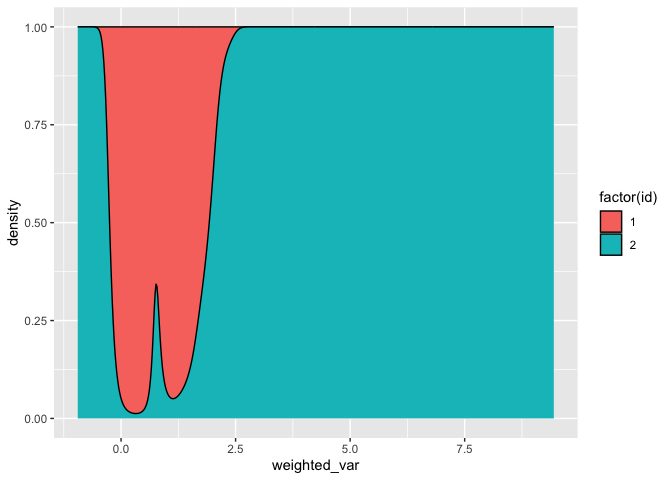
# Fill
df %>%
  mutate(weighted_var = var*weight) %>%
  ggplot(aes(x = weighted_var, fill = factor(id), group = id))  
  geom_density(position = 'fill')

^{Created on 2022-11-01 with reprex v2.0.2}