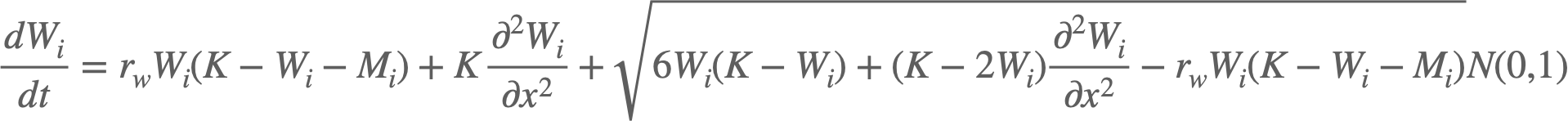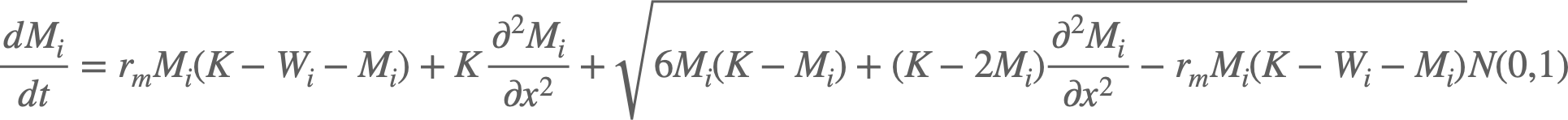Julia Stochastic Differential Equation Very Slow-CodePudding

Please help me figure out why my code is sooo slow and possible ways to speed it up. I have used vectorization, @inbounds, column major indexing, @floop, and preallocation so I would think it would be faster. I am at a loss...

The code simulates a stochastic wave of cells (as in biological cells) and mutant cells. I am using the Euler-Murayama method to propagate the coupled (Chemical Langevin) equations:

Where W/M denotes the number of wild-type cells and mutant cells respectively, K is the carrying capacity (maximum number of cells), i denotes the deme (location), and N(0,1) is a normal random variable.

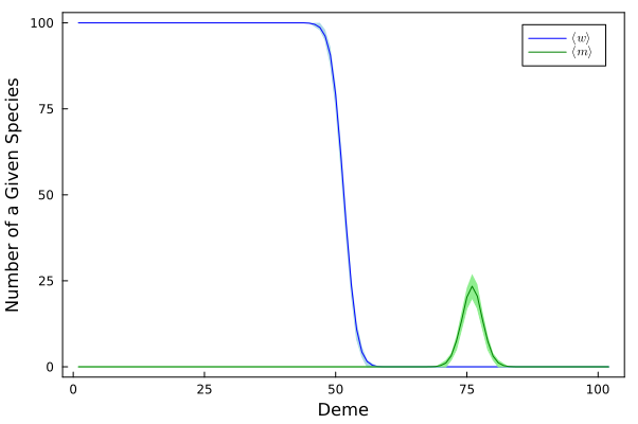
Here is a graphic of the waves after some time propagating:

I have attached the important part of the code below, and tried to comment it as best as I could.

using Random, Distributions
using StatsBase
using Statistics
using FLoops

# CLE Parameters/Set-Up:
K = 100 # Carrying capacity (maximum number of cells)
M = 100 # Number of demes (locations)
T = 100_000_000 # number of time steps
dt = 1e-1 # time increment
g = Normal(0.0,sqrt(dt)) # normal distribution with ave = 0.0, std_dev = dt
r_w = 0.1 # Wild-type growth rate
r_m = 0.2 # Mutant growth rate
r_wm = [r_w, r_m]' # Growth rate vector (transposed)
N = 1 # number of independent processes (slow even when N = 1)

# initial wave (essentially a step-function of wild-types 
# with 100 mutants at deme (location) 76)
state_init = Matrix(reshape(repeat([K, 0.0]',M 2),(M 2,2))) 
state_init[M÷2 2:end,1] .= 0   
state_init[76,2] = 100.0
state_init[1,:] .= [K,0]
state_init[end,:] .= [0,0]

state = deepcopy(state_init)
state_plus = zeros(size(state_init)) # state at demes i 1 instead of i (used for derivatives)
state_minus = zeros(size(state_init)) # state at demes i-1 instead of i (used for derivatives)

function sim!(state_init::Matrix{Float64}, state::Matrix{Float64},
              T::Int64, dt::Float64, N::Int64, M::Int64, K::Int64,
              hist_data::Array{Int64,3}, g::Normal{Float64})

    @inbounds @floop for n in 1:N
        state .= deepcopy(state_init) # initialize state
        @inbounds for t in 1:T
            
            state_plus .= circshift(state, -1) # make plus state
            state_plus[1,:] .= [0,0] # fix boundary conditions
            state_minus .= circshift(state, 1) # make minus state
            state_minus[end,:] .= [0,0] # fix boundary conditions
            state_shift = circshift(state, (0,1)) 
            # make state where each deme has a vector 
            # (# mutants, # wild-types) instead of 
            # (# wild-types, # mutants)

            ######################################
            # propagate state using Euler-Murayama method and
            # restrict number of cells in a deme to be in the range [0,K]
            # using clamp(). clamp() also prevents imaginary numbers from 
            # a negative number under the sqrt().

            state .= clamp.(state .  
            dt .* (r_wm .* state .* (K .- state .- state_shift) .  
            K .* (state_plus .- 2.0 .* state .  state_minus)) .  
            sqrt.(clamp.(
            6 .* state .* (K .- state) .  
            (K .- 2.0 .* state) .* (state_plus .- 2.0 .* state .  
            state_minus) .- r_wm .* state .* (K .- state .- state_shift), 
            0.0, 1.0*K*K)) .* 
            rand(g,M 2), 0.0, 1.0*K) 
            ######################################

        end
    end
end

sim!(state_init, state, T, dt, N, M, K, hist_data, g)


... the rest of the code is analysis and not the reason the code is slow.

CodePudding user response：

Even though you're pre-allocating state_plus and state_minus, memory is being allocated inside the for loop since you're using circshift instead of circshift!. circshift allocates new memory regardless of the fact that it's ultimately being assigned to an existing pre-allocated array. Doing that allocation 300 million times is bound to be costly!

Try

function sim!(state_init::Matrix{Float64}, state::Matrix{Float64},
              T::Int64, dt::Float64, N::Int64, M::Int64, K::Int64,
              hist_data::Array{Int64,3}, g::Normal{Float64})

    @inbounds @floop for n in 1:N
        state .= deepcopy(state_init) # initialize state
        state_plus = zeros(size(state_init)) # state at demes i 1 instead of i (used for derivatives)
        state_minus = zeros(size(state_init)) # state at demes i-1 instead of i (used for derivatives)
        state_shift = zeros(size(state_init)) 

        for t in 1:T
            
            circshift!(state_plus, state, -1) # make plus state
            state_plus[1,:] .= [0,0] # fix boundary conditions
            circshift!(state_minus, state, 1) # make minus state
            state_minus[end,:] .= [0,0] # fix boundary conditions
            circshift!(state_shift, state, (0,1))

and

function sim!(state_init::Matrix{Float64}, state::Matrix{Float64},
              T::Int64, dt::Float64, N::Int64, M::Int64, K::Int64,
              hist_data::Array{Int64,3}, g::Normal{Float64})

    state_plus = zeros(size(state_init)) # state at demes i 1 instead of i (used for derivatives)
    state_minus = zeros(size(state_init)) # state at demes i-1 instead of i (used for derivatives)
    state_shift = zeros(size(state_init)) 
    @inbounds for n in 1:N
        state .= deepcopy(state_init) # initialize state
        for t in 1:T
            
            circshift!(state_plus, state, -1) # make plus state
            state_plus[1,:] .= [0,0] # fix boundary conditions
            circshift!(state_minus, state, 1) # make minus state
            state_minus[end,:] .= [0,0] # fix boundary conditions
            circshift!(state_shift, state, (0,1))

The second version doesn't use @floop, but that allows it to not have to initialize state_plus and others N times, so it may be the case that it's faster for your actual N. Best to try both and find out!