Find optimal (smallest) convex hull around a portion of a large dataset in Python-CodePudding

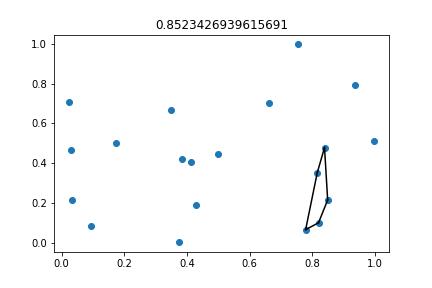
I have many (x, y) points. I want to fit the smallest (or an approximation or estimation of the smallest) convex hull around a variable percentage of those points.

The existing implementations I can find get the convex hull around all the points. How can I have a function like so:

def get_convec_hull(points, percentage):
    # some code here
    return smallest_hull

I can brute force my desired outcome using the code below. This does exactly what I want, except that it's really slow. Finding the smallest convex hull around a portion of 25% of 40 data points already takes a couple of sections. My real data has many million points.

# A brute force solution..

from scipy.spatial import ConvexHull
import itertools

import numpy as np
import math

np.random.seed(11111)

# Simulating my data..
n_points = 20
target_percentage = 0.25
points = np.random.random((n_points, 2))

def get_convec_hull(points, percentage):
    n_points = points.shape[0]
    target_points = int(n_points * percentage)
    print("Looking for smallest polygon covering {} of the {} datapoints!".format(target_points, n_points))
    print(target_points)

    subsets = itertools.combinations(list(range(n_points)), target_points)

    optimal = ConvexHull(points[next(subsets),:]) # first one designated as optimal at the start
    for subset in subsets:
        hull = ConvexHull(points[subset,:])
        if hull.area < optimal.area:
            optimal = hull

    return optimal


optimal = get_convec_hull(points, target_percentage) 
optimal.area # returns 0.85234...

Also, just to illustrate, this is the 'optimal', i.e., the smallest convex hull around 25% (5 points) for the simulated dataset.

How could I apply this to a much larger dataset?

CodePudding user response：

Please realize I am risking my life posting this; I am fairly certain actual computer scientists are already tracing my IP.

I have rewritten your function in the following manner:

def get_suboptimal_hull(points,p,magic_number):
    n_points = points.shape[0]
    tp = int(n_points * p)
    
    d_mat = distance_matrix(points,points)
    d_mat_s = d_mat.copy()
    d_mat_s.sort(axis=1)
    
    dist = np.sum(d_mat_s[:,0:5],axis=1)
    dens = d_mat_s[:,4]/(dist**2)
    densstr = [str(x)[0:4] for x in dens]
    dens_s = dens.copy()
    dens_s.sort()

    mnp = -1 * int(magic_number*points.shape[0]) - 1
    suboptimal = points[dens > dens_s[mnp]]
        
    n_points = len(suboptimal)
    
    subsets = itertools.combinations(list(range(n_points)), tp)

    optimal = ConvexHull(suboptimal[next(subsets),:])
    for subset in subsets:
        hull = ConvexHull(suboptimal[subset,:])
        if hull.area < optimal.area:
            optimal = hull

    return optimal

The way I achieve the speedup is by "cleverly" pruning the point tree based on a density parameter. By pruning the tree with a divisor of magic_number, you can achieve a magic_number^2 divisor speedup (tree generation is N^2). There are two things to take care of:

I still use your function to approach the optimal value
The speedup and performance is heavily dependent on the value of magic_number.

Currently, magic_number is a percentage of the points, but could just as easily be modified as a fixed number to stabilize performance. Might be useful for your applications.

Init:

from scipy.spatial import ConvexHull
from scipy.spatial import distance_matrix
import itertools
import numpy as np
import math
import matplotlib.pyplot as plt

np.random.seed(11111)

n_points = 20
target_percentage = 0.25
points = np.random.random((n_points, 2))
magic_number = 0.5

The area is the same (there could be exceptions where is is not true, methinks):

optimal = get_convec_hull(points, target_percentage) 
suboptimal = get_suboptimal_hull(points, target_percentage,0.5)
print((optimal.area, suboptimal.area))

Returns:

(0.8523426939615691, 0.8523426939615691)

(I noticed that in this configuration, this is perimeter. Still the same tough.)

Speedup:

yours = %timeit -r 3 -o get_convec_hull(points, target_percentage)
mine = %timeit -r 3 -o get_suboptimal_hull(points, target_percentage,magic_number)
your_t = np.mean(yours.all_runs)
my_t = np.mean(mine.all_runs)
print(f'For magic number {magic_number}, expected {int(100*(1/magic_number**2))} % speedup, got a {int(100* (your_t/my_t))} % speedup.')

Returns:

8.44 s ± 162 ms per loop (mean ± std. dev. of 3 runs, 1 loop each)
143 ms ± 1.67 ms per loop (mean ± std. dev. of 3 runs, 10 loops each)
For magic number 0.5, expected 400 % speedup, got a 590 % speedup.