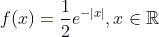Why is geom_density plotting my data differently from the expected image?-CodePudding

I have the following task statement:

In this task we want to simulate random variables with density

To do this, write a function r_density(n) that simulates n of such random variables. Then use this function to simulate N = 1000 of such random variables. Using geom_density() you can now estimate the density from the simulated random variables. We can compare this estimate with the real density. To do this, create a graph that looks like this:

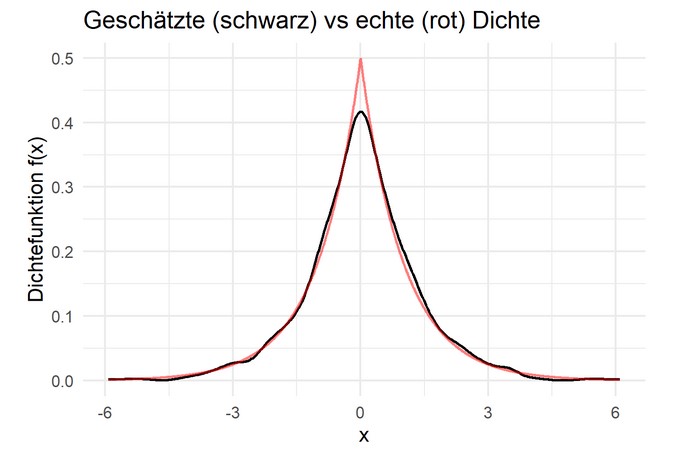
Problem is, however, that I don't understand why my output looks like this:

Why is the raked density plotted in such a weird way? Can someone explain to me why it looks like that and how to get the estimated density from the expected image?

This is the corresponding code I wrote for the above plot:

library(tidyverse)

N <- 1000

r_density <- function(n){
  exp(-abs(n))/2
}

x <- runif(N)

tb <- tibble(
  x = x,
  density_fkt = r_density(x)
)

ggplot()  
  geom_density(
    data = tb,
    mapping = aes(
      x = density_fkt,
      y = ..scaled..
    )
  )  
  geom_function(
    fun = r_density,
    xlim = c(-6,6),
    color = "red",
    size = 1
  )  
  theme_minimal()  
  labs(
  x = "x",
  y = "Dichtefunktion f(x)",
  title = "Geschätzte (schwarz) vs echte (rot) Dichte"
  )

CodePudding user response：

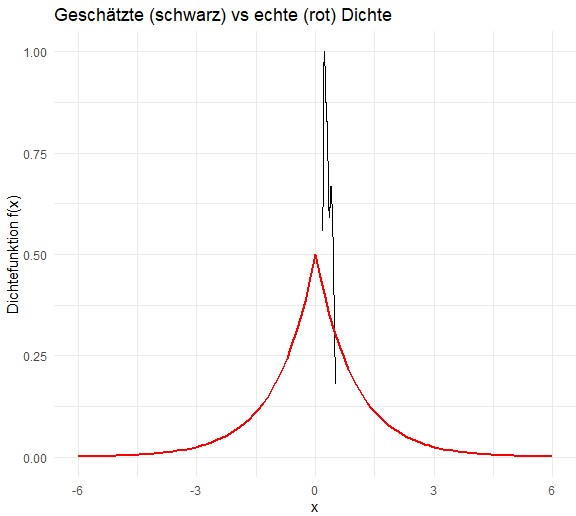
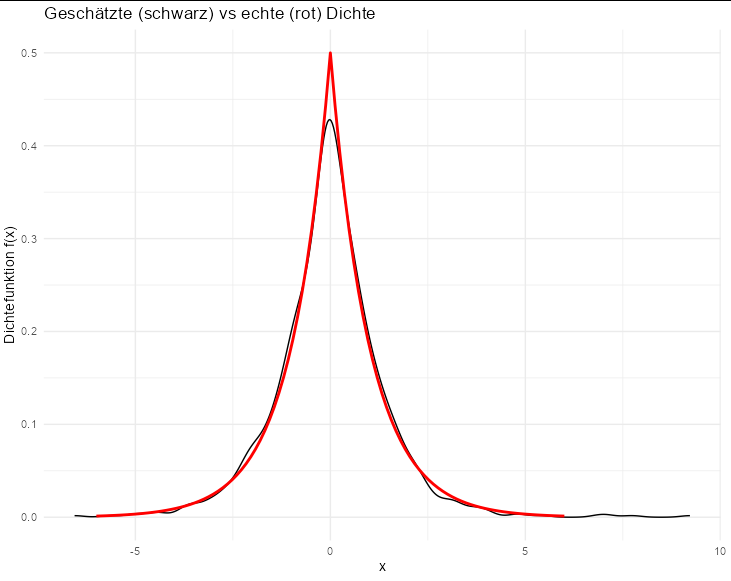
You may use inverse transform sampling or rejection sampling. I choose rejection sampling.

library(tidyverse)

N <- 1000

r_density <- function(n){
  exp(-abs(n))/2
}

x = c()
while (length(x) < N) {
  y = rnorm(1)
  while (y > 6 | y < -6) {
    y = rnorm(1)
  }
  u = runif(1)
  if (u < r_density(y)/(dnorm(y) * 3)) {
    x=append(x, y)
  }
}


tb <- tibble(
  x = x,
  density_fkt = r_density(x)
)

ggplot()  
  geom_density(
    data = tb,
    mapping = aes(
      x = x,
      y = ..density..
    )
  )  
  geom_function(
    fun = r_density,
    xlim = c(-6,6),
    color = "red",
    size = 1
  )  
  theme_minimal()  
  labs(
    x = "x",
    y = "Dichtefunktion f(x)",
    title = "Geschätzte (schwarz) vs echte (rot) Dichte"
  )

CodePudding user response：

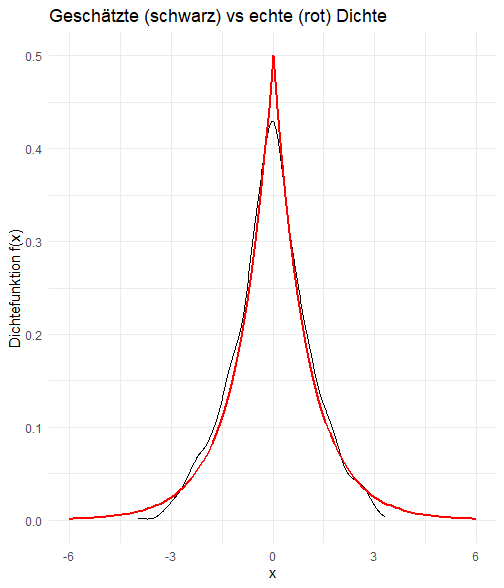
Here's the inverse transform sampling method (this involves some difficult integration, so perhaps not what your teacher intended)

r_density <- function(n) {

  cdf <- function(x) {
      1/4 * exp(-x) * (-1   2 * exp(x)   exp(2*x) - (-1   exp(x))^2 * sign(x))
  }

  sapply(runif(n), function(i) {
  uniroot(function(x) cdf(x) - i, c(-30, 20))$root
  })
}

Plotting gives:

ggplot()  
  geom_density(aes(r_density(1000)))  
  geom_function(
    fun = function(x) exp(-abs(x))/2,
    xlim = c(-6,6),
    color = "red",
    size = 1
  )  
  theme_minimal()  
  labs(
    x = "x",
    y = "Dichtefunktion f(x)",
    title = "Geschätzte (schwarz) vs echte (rot) Dichte"
  )