Splitting the range of colorbar in Python-CodePudding

In the following code, I am representing the data through array X on different colors. But I want to limit the number of colors to 6 (and not 8 as shown in the output) with each range being 100. Is there a way to do it?

import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
import numpy as np
from matplotlib.colors import Normalize
from matplotlib import cm
import math
from  numpy import nan

fig,ax = plt.subplots(1)
n=3


N=2*n*(n-1)


J=[[3, 6, 7, 8, 9, 10, 11]]

J[0].sort()
              
XI=np.array([[0, 1, 2, 4, 5]])

X=np.array([[100.1,200.9,304.5,430.9,578.6]])

C1 = nan

print("J[0] =",J)

for i in J[0]:
    X = np.insert(X, i, [C1], axis=1)
print("X =", [X])

Amin=0
Amax=600.0


color = cm.get_cmap('Dark2')
norm = Normalize(vmin=Amin, vmax=Amax)
color_list = []
for i in range(len(X[0])):
    color_list.append(color((X[0,i]-Amin)/(Amax-Amin)))
    
#print(color_list)
id = 0
for j in range(0, n):
    for k in range(n-1):
        ax.hlines(200 200*(n-j-1) 5*n, 200*(k 1) 5*n, 200*(k 2) 5*n, zorder=0, linewidth=5.0,colors=color_list[id])
        id  = 1

    for i in range(0, n):
        rect = mpl.patches.Rectangle((200 200*i, 200 200*j), 10*n, 10*n, linewidth=1, edgecolor='black', facecolor='black')
        ax.add_patch(rect)
        if j < n-1:
            ax.vlines(200 200*i 5*n, 200*(n-1-j) 5*n, 200*(n-j) 5*n, zorder=0, linewidth=5.0, colors=color_list[id])
            id  = 1

cb = fig.colorbar(cm.ScalarMappable(cmap=color, norm=norm))
cb.set_ticks(np.arange(Amin, Amax 0.1e-05, (Amax-Amin)/6).astype(float))
cb.set_label("\u0394P (N/m$^{2}$)")
ax.set_xlim(left = 0, right = 220*n)
ax.set_ylim(bottom = 0, top = 220*n)

# ax.set_yticklabels([])
# ax.set_xticklabels([])
plt.axis('off')
plt.title("Time = 0.0",fontsize=20)
plt.show()

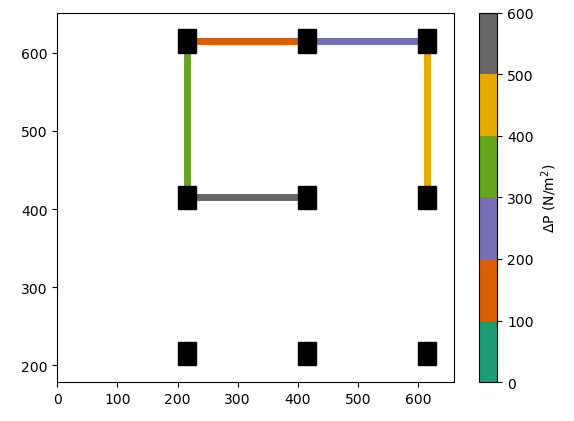
The present output is

from matplotlib.colors import BoundaryNorm
import numpy as np

norm = BoundaryNorm(np.arange(Amin, Amax 1, 100), color.N)

The normalizer above sets the amount of colors to the length of the colormap, this causes it to sample the 6 colors (defined by the boundaries) to be stretched along the entire map, from first to last. Setting it to 6 would for example use the first 6 colors.

Using the above normalizer, the result looks like: