Generating three new features (membership class) based on probability clustering-CodePudding

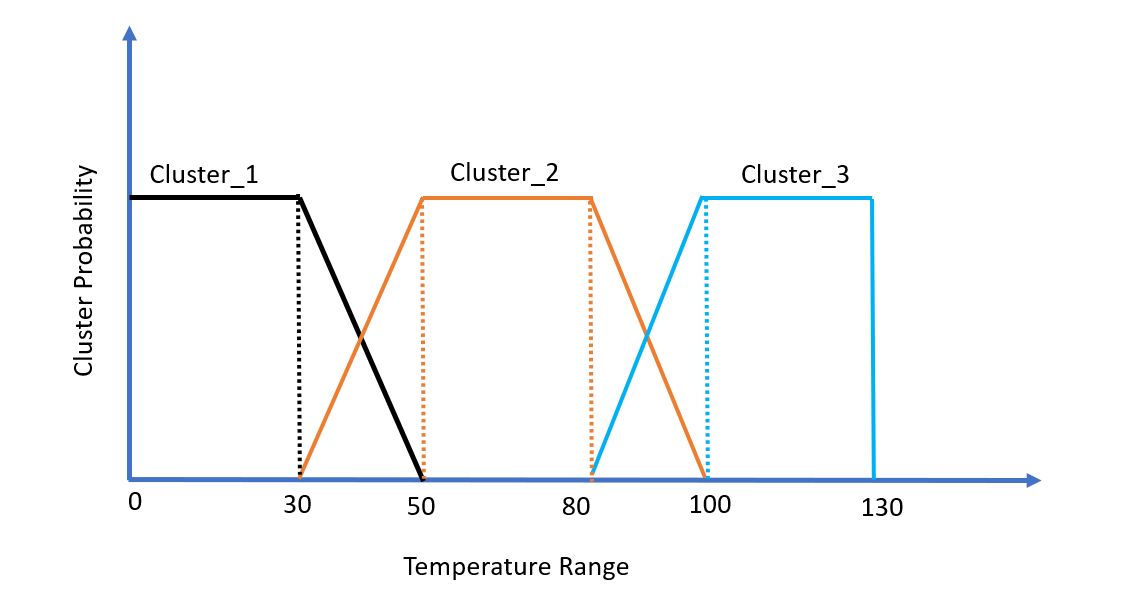
I have a column of 100,000 temperatures with a minimum of 0°F and maximum of 130°F. I want to create three new columns (features) based on that temperature column for my model based on probability of membership to a cluster (I think it is also called fuzzy clustering or soft k means clustering).

As illustrated in the plot below: I want to create 3 class memberships with overlap (cold, medium, hot) each with probability of data points belonging to each class of temperature. For example: a temperature of 39°F might have a class 1 (hot) membership of 0.05, a class 2 (medium) membership of 0.20 and a class 3 (cold) membership of 0.75 (note the sum of three would be 1). Is there any way to do this in Python?

  cluster_1 = 0 to 30
  Cluster_2 = 50 to 80
  Cluster_3 = 100 to 130

CodePudding user response：

Based on the image and description: this is more of an assignment problem based on known soft clusters, rather than a clustering problem in itself.

If you have a vector of temperatures: [20, 30, 40, 50, 60, ...] that you want to convert to probabilities of being cold, warm, or hot based on the image above, you can achieve this with linear interpolation:

import numpy as np

def discretize(vec):
    out = np.zeros((len(vec), 3))

    for i, v in enumerate(vec):
        if v < 30:
            out[i] = [1.0, 0.0, 0.0]
        elif v <= 50:
            out[i] = [(50 - v) / 20, (v - 30) / 20, 0.0]
        elif v <= 80:
            out[i] = [0.0, 1.0, 0.0]
        elif v <= 100:
            out[i] = [0.0, (100 - v) / 20, (v - 80) / 20]
        else:
            out[i] = [0.0, 0.0, 1.0]

    return out

result = discretize(np.arange(20, 120, step=5))

Which will expand a 1xN array into a 3xN array:

[[1.   0.   0.  ]
 [1.   0.   0.  ]
 [1.   0.   0.  ]
 [0.75 0.25 0.  ]
 [0.5  0.5  0.  ]
 [0.25 0.75 0.  ]
 [0.   1.   0.  ]
  ...
 [0.   1.   0.  ]
 [0.   0.75 0.25]
 [0.   0.5  0.5 ]
 [0.   0.25 0.75]
 [0.   0.   1.  ]
  ...
 [0.   0.   1.  ]]

If you don't know the clusters ahead of time, a Gaussian mixture performs something similar to this idea.

For example, consider a multimodal distribution X with modes at 25, 65, and 115 (to correspond roughly with the temperature example):

from numpy.random import default_rng

rng = default_rng(42)

X = np.c_[
    rng.normal(loc=25, scale=15, size=1000),
    rng.normal(loc=65, scale=15, size=1000),
    rng.normal(loc=115, scale=15, size=1000),
].reshape(-1, 1)

Fitting a Gaussian mixture corresponds to trying to estimate where the means are:

model = GaussianMixture(n_components=3, random_state=42)
model.fit(X)

print(model.means_)

Here: the means that are found tend to be pretty close to where we expected them to be in our synthetic data:

[[115.85580935]
 [ 25.33925571]
 [ 65.35465989]]

Finally, the .predict_proba() method provides an estimate for how likely a value belongs to each cluster:

>>> np.round(model.predict_proba(X), 3)
array([[0.   , 0.962, 0.038],
       [0.002, 0.035, 0.963],
       [0.989, 0.   , 0.011],
       ...,
       [0.   , 0.844, 0.156],
       [0.88 , 0.   , 0.12 ],
       [0.993, 0.   , 0.007]])