How to optimize the zoom parameter in zoomed_inset

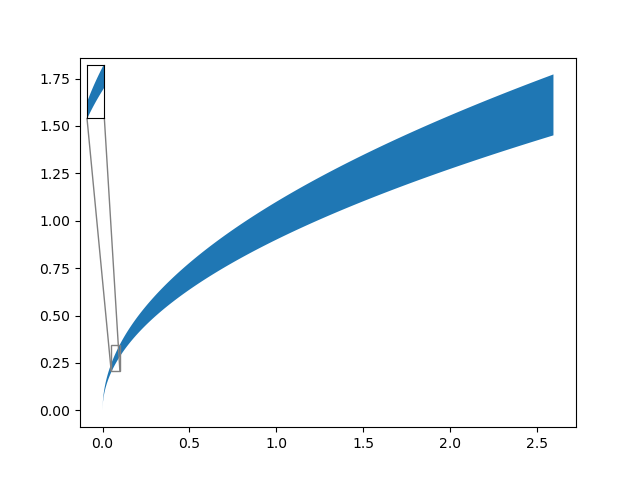
I am creating plots that include zoom inserts. The data is diverse it is impossoble for me to know what the data will be like before the program starts. I want to make the zoom insert zoom in as much as possible, without overlapping with any other element of my plot. Here is an example, where I use a zoom of 2. Ideally, I would like to automatically determine what this number should be:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1.inset_locator import zoomed_inset_axes
from mpl_toolkits.axes_grid1.inset_locator import mark_inset

fig, ax = plt.subplots()

xin = np.linspace(0, np.random.uniform(.5, 4), 1000)    
x_samples = np.random.uniform(0.9, 1.1, (1, 1000)) * np.sqrt(xin[:, np.newaxis])

ax.fill_between(xin, x_samples.min(1), x_samples.max(1))

axins = zoomed_inset_axes(ax, zoom=2, loc='upper left')
axins.fill_between(xin, x_samples.min(1), x_samples.max(1))
axins.set_xlim(.05, .1)
idx = np.logical_and(xin > 0.05, xin < 0.1)
axins.set_ylim(x_samples.min(1)[idx].min(), x_samples.max(1)[idx].max())
axins.set_xticks([])
axins.set_yticks([])

mark_inset(ax, axins, loc1=4, loc2=3, fc="none", ec="0.5")

plt.savefig('hey')
plt.clf()

As you can see, zoom=2 was too low of a value. I can manually set the zoom parameter to a correct value. This is a tedious process. Is there a way to automatically find the zoom parameter that will maximize the insert size while avoiding overlaps with other parts of the plot?

CodePudding user response：

We can face this problem in an iterative way:

Start with the maximum possible zoom (such that the inset occupies the whole height of the plot). As a result, part of the inset will overlap the plot.
Check how much vertical gap exists before the point where the overlapping starts.
Based on the current height of the inset, scale it down to avoid overlapping.
After the rescaling, the width of the inset is also reduced, so we can scale it up again with the free vertical gap that has been left behind.
Go back to 2. until convergence / maximum number of iterations is reached.

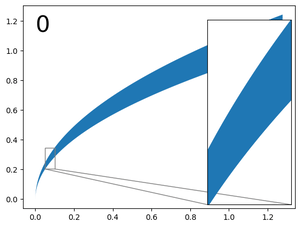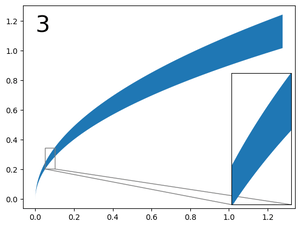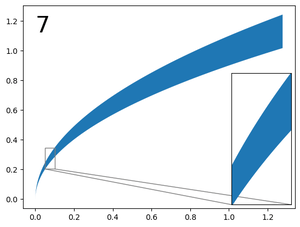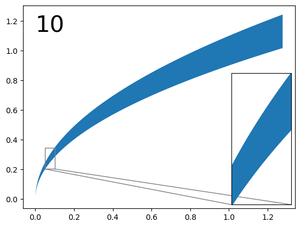
In practice the convergence is fast and reached in less than 10 iterations with the given data.

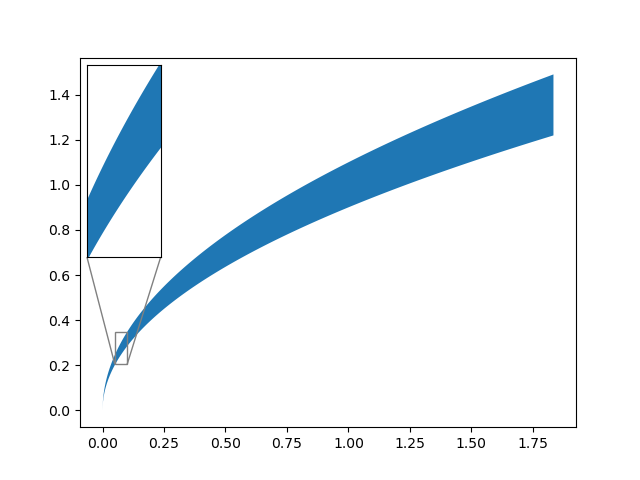
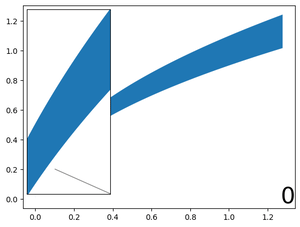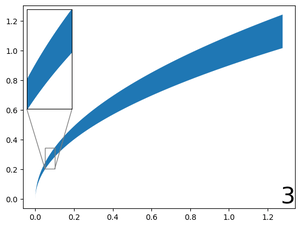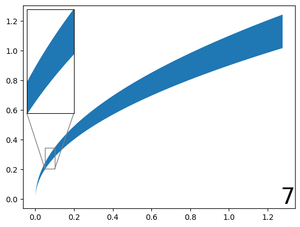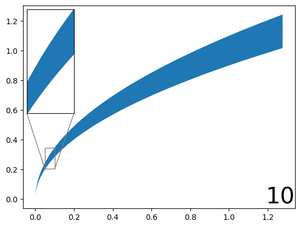
Visually:

Code for insets at the upper-left location.

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1.inset_locator import zoomed_inset_axes, mark_inset


def get_inset_max_zoom(x, y, xlim_inset, ylim_inset, max_iters=10):
    """ Zoom that maximizes inset size without overlapping the artists """
    # width and height of the inset in non-scaled coordinates.
    inset_w = xlim_inset[1] - xlim_inset[0]
    inset_h = ylim_inset[1] - ylim_inset[0]

    # max y-coordinate of the whole plot.
    y_max_plot = y.max()

    # start with maximum zoom.
    y_gap = y_max_plot - y.min()
    zoom = y_gap / inset_h

    for i in range(max_iters):
        y_affected_max = y[x < zoom * inset_w].max()

        # recalculate zoom by adjusting the gap.
        y_gap = y_max_plot - y_affected_max
        zoom = y_gap / inset_h

    return zoom


if __name__ == "__main__":
    # Change the seed to show produce different values.
    rng = np.random.RandomState(seed=0)

    # main plot.
    fig, ax = plt.subplots()
    xin = np.linspace(0, rng.uniform(.5, 4), 1000)
    x_samples = rng.uniform(
        0.9, 1.1, (1, 1000)) * np.sqrt(xin[:, np.newaxis])
    ax.fill_between(xin, x_samples.min(1), x_samples.max(1))

    # get xy pairs.
    y = x_samples.ravel()
    x = np.repeat(xin, x_samples.shape[1])

    # define the limits and location of the zoom inset.
    xlim_inset = (.05, .1)
    idx = np.logical_and(xin > xlim_inset[0], xin < xlim_inset[1])
    ylim_inset = (x_samples.min(1)[idx].min(), x_samples.max(1)[idx].max())
    loc = 'upper left'

    # get max zoom.
    zoom = get_inset_max_zoom(x, y, xlim_inset, ylim_inset, max_iters=5)

    # create the inset.
    axins = zoomed_inset_axes(ax, zoom=zoom, loc=loc, borderpad=0.5)
    axins.set(
        xlim=xlim_inset,
        ylim=ylim_inset,
        xticks=[], yticks=[])

    # connect the bboxes.
    mark_inset(ax, axins, loc1=4, loc2=3, fc="none", ec="0.5")
    # plot within the inset.
    axins.fill_between(xin, x_samples.min(1), x_samples.max(1))

Generalizing to the 4 corner locations {upper-left, upper-right, lower-right, lower-left}. For instance, with loc = 'lower right':

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1.inset_locator import zoomed_inset_axes, mark_inset


def get_inset_max_zoom_given_loc(
        x, y, xlim_inset, ylim_inset, loc='upper left', max_iters=10):
    """ Zoom that maximizes inset size without overlapping the artists """
    # width and height of the inset in non-scaled coordinates.
    inset_w = xlim_inset[1] - xlim_inset[0]
    inset_h = ylim_inset[1] - ylim_inset[0]

    # handy variables.
    is_left = 'left' in loc
    is_upper = 'upper' in loc

    y_min_plot, y_max_plot = y.min(), y.max()
    y_xtm_plot = y_max_plot if is_upper else y_min_plot
    x_max_plot = x.max()

    # start with maximum zoom.
    y_gap = y_max_plot - y_min_plot
    zoom = y_gap / inset_h

    for i in range(max_iters):
        # get affected x-coordinate range.
        if is_left:
            x_affected = x < zoom * inset_w
        else:
            x_affected = x > x_max_plot - zoom * inset_w

        # get affected y-coordinate extremum.
        y_affected = y[x_affected]
        y_affected_xtm = y_affected.max() if is_upper else y_affected.min()

        # recalculate zoom by adjusting the gap.
        y_gap = abs(y_xtm_plot - y_affected_xtm)
        zoom = y_gap / inset_h

    return zoom


if __name__ == "__main__":
    # Change the seed to show produce different values.
    rng = np.random.RandomState(seed=0)

    # main plot.
    fig, ax = plt.subplots()
    xin = np.linspace(0, rng.uniform(.5, 4), 1000)
    x_samples = rng.uniform(
        0.9, 1.1, (1, 1000)) * np.sqrt(xin[:, np.newaxis])
    ax.fill_between(xin, x_samples.min(1), x_samples.max(1))

    # get xy pairs.
    y = x_samples.ravel()
    x = np.repeat(xin, x_samples.shape[1])

    # define the limits and location of the zoom inset.
    xlim_inset = (.05, .1)
    idx = np.logical_and(xin > xlim_inset[0], xin < xlim_inset[1])
    ylim_inset = (x_samples.min(1)[idx].min(), x_samples.max(1)[idx].max())
    loc = 'lower right'

    # get max zoom.
    zoom = get_inset_max_zoom_given_loc(
        x, y, xlim_inset, ylim_inset, loc=loc, max_iters=10)

    # create the inset.
    axins = zoomed_inset_axes(ax, zoom=zoom, loc=loc, borderpad=0.5)
    axins.set(
        xlim=xlim_inset,
        ylim=ylim_inset,
        xticks=[], yticks=[])

    # connect the bboxes.
    mark_inset(ax, axins, loc1=4, loc2=3, fc="none", ec="0.5")
    # plot within the inset.
    axins.fill_between(xin, x_samples.min(1), x_samples.max(1))