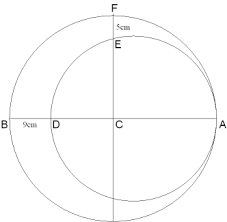
I am struggling to find a way to get Random positions within a Crescent area. Calculating the crescent is well documented using the difference of two overlapping circles. But that calculates the surface area, which is not enough if I want to generate random positions in that area.

In this illustration we know both the center origin points and radii:

CenterPoint of CircleA ca=0,0 Radius of ca caRad = 100
CenterPoint of CircleB cb=9,0 Radius of cb cbRad = 85

knowing these values we could fill in all the variables on the illustration; A, B, D, E and F. Calculating the Crescent Area would be

π*(caRad²) - π*(cbRad²) = 2775π

And this is where I am stuck, I have all the information yet, don't know on how to proceed getting random positions 'Within' that crescent area.

Any help in this matter is very appreciated, Nick.

CodePudding user response：

Repeat generating random points in the outer circle (in the full area of it) by generating points in the bounding square until a point is in the outer circle but not within the inner circle.

float caRad = 100;
float cbRad = 85;
var ca = new PointF(0, 0);
var cb = new PointF(caRad - cbRad, 0); // = (15, 0), because with (9, 0) the inner
                                       // circle would not touch the outer circle.
var random = new Random();
PointF p;
do {
    p = new PointF(
        ca.X   2 * caRad * random.NextSingle() - caRad,
        ca.Y   2 * caRad * random.NextSingle() - caRad
    );
    PointF da = p - ca;
    PointF db = p - cb;
} while (da.X * da.X   da.Y * da.Y > caRad * caRad || // while p not in ca OR
         db.X * db.X   db.Y * db.Y <= cbRad * cbRad);  // p in cb
// Here the random point p is in ca but not in cb.

The while-condition calculates the square of the Euclidean distance of the point to the center of the circles and compares it to the square of the radii of the circles to determine whether a point is within a circle or not. The calculation of the Euclidean distance is based on the Pythagorean theorem.

We use the square root function to get the real distance, but is cheaper to calculate the square of the radii instead.

CodePudding user response：

If circle radii are not too close, then you can generate random point inside larger circle, then check if point is outside of the smaller circle. If not, repeat generation.

a = random()*2*Pi
r = R1*sqrt(random())
x = cx   r*cos(a)
y = cy   r*sin(a)
if (x-c2x)^2 (y-c2y)^2 >= R2^2:
     point in crescent

For almost equal circles (very small crescent area) this method is not effective. In this case one could generate random angle in 0..2Pi range with cosine (non-uniform) distribution, then get radius in range corresponding to this angle.

CodePudding user response：

It's not necessarily cheap, and I don't think it distributes uniformly if you really care about that, but you can:

1. Generate a random point on the boundary of the inner circle (i.e. generate a random angle from 0 to 360)

2. Draw a line from the center of the inner circle to the point on the boundary you rolled, then continue that line until it hits the boundary of the outer circle (don't actually draw it, just conceptualize it)

3. Generate a random point on the part of that line which is outside the inner circle and inside the outer circle