Clipping a datatime series along the y-axis-CodePudding

I have a list of tuples, where each tuple is a datetime and float. I wish to clip the float values so that they are all above a threshold value. For example if I have:

a = [
    (datetime.datetime(2021, 11, 1, 0, 0, tzinfo=tzutc()), 100), 
    (datetime.datetime(2021, 11, 1, 1, 0, tzinfo=tzutc()), 9.0), 
    (datetime.datetime(2021, 11, 1, 2, 0, tzinfo=tzutc()), 100.0)
]

and if I want to clip at 10.0, this would give me:

b = [
    (datetime.datetime(2021, 11, 1, 0, 0, tzinfo=tzutc()), 100), 
    (datetime.datetime(2021, 11, 1, 0, ?, tzinfo=tzutc()), 10.0), 
    (datetime.datetime(2021, 11, 1, 1, ?, tzinfo=tzutc()), 10.0), 
    (datetime.datetime(2021, 11, 1, 2, 0, tzinfo=tzutc()), 100.0)
]

So if I were to plot the a data (before clipping), I would get a V shaped graph. However, if I clip the data at 10.0 to give me the b data, and plot, I will have a \_/ shaped graph instead. There is a bit of math involved in calculating the new times so I'm hoping there is already functionality available to do this kind of thing. The datetimes are sorted in order and are unique. I can fix the data so the difference between consecutive times is equal, should that be necessary.

CodePudding user response：

Apologies for not putting a full answer yesterday, my SO account is still rate-limited.

I have made a bit more complex custom dataset to showcase several values in a row being below threshold.

import pandas as pd
from datetime import datetime
from matplotlib import pyplot as plt
from scipy.interpolate import InterpolatedUnivariateSpline

df = pd.DataFrame([
    (datetime(2021, 10, 31, 23, 0), 0),
    (datetime(2021, 11, 1, 0, 0), 80),    
    (datetime(2021, 11, 1, 1, 0), 100), 
    (datetime(2021, 11, 1, 2, 0), 6), 
    (datetime(2021, 11, 1, 3, 0), 105),
    (datetime(2021, 11, 1, 4, 0), 70),
    (datetime(2021, 11, 1, 5, 0), 200),
    (datetime(2021, 11, 1, 6, 0), 0),
    (datetime(2021, 11, 1, 7, 0), 7),
    (datetime(2021, 11, 1, 8, 0), 0),
    (datetime(2021, 11, 1, 9, 0), 20),
    (datetime(2021, 11, 1, 10, 0), 100),
    (datetime(2021, 11, 1, 11, 0), 0)
], columns=['time', 'whatever'])

THRESHOLD = 10

The first thing to do here is to express index in terms of timedelta so that it behaves as any usual number we can then do all kinds of calculations with. For convenience, I am also expressing it as Series - an even better approach would be to create it as such from the get go, save the initial timestamp and reindex.

start_time = df['time'][0]
df.set_index((df['time'] - start_time).dt.total_seconds(), inplace=True)
series = df['whatever']

Then, I've tried InterpolatedUnivariateSpline from scipy:

roots = InterpolatedUnivariateSpline(df.index, series.values - THRESHOLD).roots()
threshold_crossings = pd.Series([THRESHOLD] * len(roots), index=roots)
new_series = pd.concat([series[series > THRESHOLD], threshold_crossings]).sort_index()

Let's test it out:

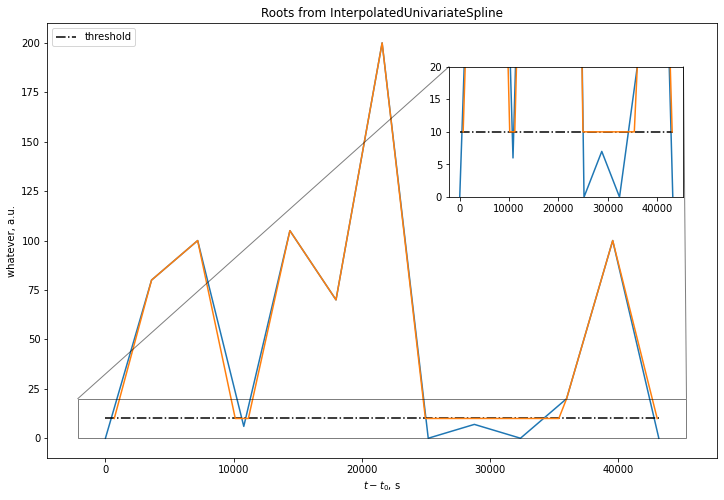
fig, ax = plt.subplots(figsize=(12, 8))
ax.plot(series)
ax.plot(df.index, [THRESHOLD] * len(df.index), 'k-.', label='threshold')
ax.plot(new_series)
ax.set_xlabel('$t-t_0$, s')
axins = ax.inset_axes([0.6, 0.6, 0.35, 0.3])
axins.plot(series)
axins.plot(df.index, [THRESHOLD] * len(df.index), 'k-.')
axins.plot(new_series)
axins.set_ylim(0, 20)
ax.indicate_inset_zoom(axins, edgecolor="black")
ax.set_ylabel('whatever, a.u.')
ax.legend(loc='upper left')
ax.set_title('Roots from InterpolatedUnivariateSpline')

Not so great. Spline roots interpolation is quite a bit off (after all, it uses a cubic B-spline under the hood and can't find roots if setting order to 1). Ah well. For monotonic functions, we could just inverse the interpolation, but this is not the case here. I hope someone finds a better way to do it, but my next step was rolling out a custom function:

def my_interp(series: pd.Series, thr: float) -> pd.Series:
    needs_interp = series > thr
    # XOR means we are only considering transition points
    needs_interp = (needs_interp ^ needs_interp.shift(-1)).fillna(False)
    # The last point will never be interpolated
    x = series.index.to_series()
    k = series.diff(periods=-1) / x.diff(periods=-1)
    b = series - k * x
    x_fill = ((thr - b) / k)[needs_interp]
    fill_series = pd.Series(data=[thr] * x_fill.size, index=x_fill.values)
    # NB! needs_interp is a wrong mask to use for series here
    return pd.concat([series[series > thr], fill_series]).sort_index()


new= my_interp(series, THRESHOLD)

It achieves what you want to do with good precision:

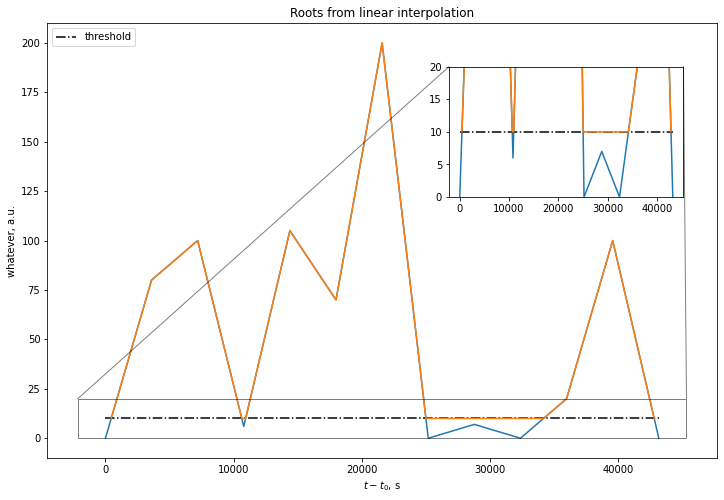
To get back to timestamp representation, one would simply do

new_series.index = (start_time   pd.to_timedelta(new_series.index, unit='s'))

With that said, there are a couple caveats:

The function above assumes the timestamps are sorted (can be achieved by sort_index), and no duplicates are present in the series
Edge conditions are nasty as usual. I have tested the function a little bit, the logic seems sound and it does not break if either side of the series is above/below the threshold, and it handles irregular data just fine, but still - watch out for NaNs in your data and consider how you should handle all the edge conditions, sorting etc.
There is no logic dedicated to handling data points exactly at threshold or ensuring there is any regularity in new timestamps. This could lead to bugs, too: e.g. if some portion of your code relies on having at least 2 data points every day, it might not hold after the transformation.