I'm given the following problem:
Create a function that takes as an input a vector of id-numbers and returns a vector of id-numbers where all incomplete experiments have been removed. The id-numbers that are not removed must remain in the same order as in the original vector.
Given vector: [1.3, 2.2, 2.3, 4.2, 5.1, 3.2, 5.3, 3.3, 2.1, 1.1, 5.2, 3.1]
Vector I need to find: [2.2, 2.3, 5.1, 3.2, 5.3, 3.3, 2.1, 5.2, 3.1]
So far, I've written this code:
import numpy as np
def removeIncomplete(id):
#round value down
np.round(id)
#saving the value
rounded = np.round(id)
# for all values in a range of length 'id'
for i in range(len(id)):
#if sample size is smaller than 3
if np.size(rounded[rounded == i]) < 3:
#remove number from array where size is smaller than 3
np.delete(rounded, np.where((rounded == i)))
return id
#testing the function
id = [1.3, 2.2, 2.3, 4.2, 5.1, 3.2, 5.3, 3.3, 2.1, 1.1, 5.2, 3.1]
print(removeIncomplete(id))
However, I need to remove the numbers which there is not 3 of, and I thought I did that by the following:
for i in range(len(id)):
#if sample size is smaller than 3
if np.size(rounded[rounded == i]) < 3:
#remove number from array where size is smaller than 3
np.delete(rounded, np.where((rounded == i)))
I somehow still get the full list, and not the one I need to get [2.2, 2.3, 5.1, 3.2, 5.3, 3.3, 2.1, 5.2, 3.1]
Where did I make a mistake as I can't seem to find it.
I've tried changing the code a little ex. adding np.delete(rounded, np.where((rounded == i) < 3)) but I can't seem to find the mistake.
CodePudding user response:
The original data you show is a list, so here's an approach without using numpy.
I was going to also add a numpy approach, but Chrysophylaxs's answer is exactly what I was typing out :)
First, let's call your input list something else, because id already means something in python.
exp_ids = [1.3, 2.2, 2.3, 4.2, 5.1, 3.2, 5.3, 3.3, 2.1, 1.1, 5.2, 3.1]
Using pure python:
Remember that it's always easier (and cheaper) to build a new list than to remove items from your existing list.
You want to find the integer smaller than the given float. Then you want to count these, and discard the original items for which the integer has a count less than 3.
First, let's count the integers. This is easy using the collections.Counter class:
import collections
exp_counts = collections.Counter(int(i) for i in exp_ids)
# Counter({1: 2, 2: 3, 4: 1, 5: 3, 3: 3})
We see that experiment 1 has two elements in the list, experiment 2 has three, and so on.
Now, we need to iterate through the original list once more, and select only those elements that have a count > 3.
filtered_ids = [i for i in exp_ids if exp_counts[int(i)] >= 3]
Which gives the desired list:
[2.2, 2.3, 5.1, 3.2, 5.3, 3.3, 2.1, 5.2, 3.1]
How to fix your code:
The answer to why you get the original array back is that np.delete returns a copy. It doesn't modify the original array, so you need to reassign to rounded if you want to modify it in the loop. Also, you need to delete those same elements from your original array, so you need another np.delete(exp_ids, ...) call like I show below.
This approach is inefficient, especially for larger arrays, because you keep creating new arrays in every iteration, which requires the entire array to be copied to a new memory location. Also, you iterate over a numpy array, which is a code-smell: numpy provides super-fast vectorized methods, so iterating over a numpy array is usually a sub-optimal way of doing the same job.
def removeIncomplete(exp_ids):
rounded = np.round(exp_ids)
# we want an element of exp_ids, not index like you do
for elem in exp_ids:
# Check where rounded is equal to the rounded element, not the index
# Since we use this multiple times, save it to a variable
filt = rounded == np.round(elem)
if filt.sum() < 3: # .sum() on a boolean array gives how many are True
# REASSIGN to the original array!!
# Need to delete from rounded AND exp_ids
# Since numpy 1.19.0, delete works with a mask like filt
exp_ids = np.delete(exp_ids, filt)
rounded = np.delete(rounded, filt)
return exp_ids
Since Chrysophylaxs provided a great numpy solution, let's do some benchmarking to compare the three approaches (I renamed yours to f_not_really_numpy):
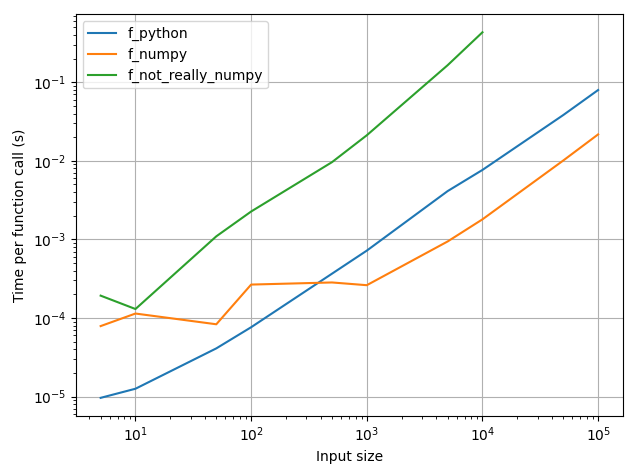
The pure-python approach is faster for inputs smaller than ~500 elements, which makes sense -- the performance gain from numpy is not worth the overhead involved in building the arrays for small inputs. You might as well get on with it and iterate in python. For larger (> 500) inputs, numpy is about 5x faster.
As you can see, your half-numpy approach is the slowest, because it is stuck with the worst of both approaches -- it needs to deal with the numpy array creation overheads, AND it iterates over the numpy arrays. Your approach is sometimes up to 50x slower than the pure-python approach, and ~100x slower than the vectorized numpy approach. I didn't have the patience to run it for an input larger than 10k elements.
If you're interested, here's the code:
import collections
import timeit
import numpy as np
from matplotlib import pyplot as plt
def time_funcs(funcs, sizes, arg_gen, N=20):
times = np.zeros((len(sizes), len(funcs)))
gdict = globals().copy()
for i, s in enumerate(sizes):
args = arg_gen(s)
print(args)
for j, f in enumerate(funcs):
gdict.update(locals())
try:
times[i, j] = timeit.timeit("f(*args)", globals=gdict, number=N) / N
print(f"{i}/{len(sizes)}, {j}/{len(funcs)}, {times[i, j]}")
except ValueError as ex:
print(args)
return times
def plot_times(times, funcs):
fig, ax = plt.subplots()
for j, f in enumerate(funcs):
ax.plot(sizes, times[:, j], label=f.__name__)
ax.set_xlabel("Array size")
ax.set_ylabel("Time per function call (s)")
ax.set_xscale("log")
ax.set_yscale("log")
ax.legend()
ax.grid()
fig.tight_layout()
return fig, ax
#%%
def arg_gen(n_rows):
n_exps = int(n_rows / 2)
exp_num = np.random.randint(1, n_exps, (n_rows,))
random_dec = np.random.random((n_rows,))
return [exp_num random_dec]
#%%
def f_python(exp_ids):
exp_counts = collections.Counter(int(i) for i in exp_ids)
return [i for i in exp_ids if exp_counts[int(i)] >= 3]
def f_numpy(arr):
rounded = np.around(arr) # Are you sure you don't want to use np.floor?
unique_elems, counts = np.unique(rounded, return_counts=True)
return arr[ np.isin(rounded, unique_elems[counts >= 3]) ]
def f_not_really_numpy(exp_ids):
rounded = np.round(exp_ids)
# we want an element of exp_ids, not index like you do
for elem in exp_ids:
# Check where rounded is equal to the rounded element, not the index
# Since we use this multiple times, save it to a variable
filt = rounded == np.round(elem)
if filt.sum() < 3: # .sum() on a boolean array gives how many are True
# REASSIGN to the original array!!
# Need to delete from rounded AND exp_ids
# Since numpy 1.19.0, delete works with a mask like filt
exp_ids = np.delete(exp_ids, filt)
rounded = np.delete(rounded, filt)
return exp_ids
#%% Set up sim
sizes = [5, 10, 50, 100, 500, 1000, 5000, 10_000, 50_000, 100_000]
funcs = [f_python, f_numpy]
funcs_small = [f_not_really_numpy]
#%% Run timing
time_fcalls = np.zeros((len(sizes), len(funcs funcs_small))) * np.nan
time_fcalls[:-2, :] = time_funcs(funcs funcs_small, sizes[:-2], arg_gen)
time_fcalls[-2:, 0:2] = time_funcs(funcs, sizes[-2:], arg_gen)
fig, ax = plot_times(time_fcalls, funcs funcs_small)
ax.set_xlabel(f"Input size")
CodePudding user response:
Here is the numpyic way to do this. Use np.unique along with np.isin:
import numpy as np
arr = np.array([1.3, 2.2, 2.3, 4.2, 5.1, 3.2, 5.3, 3.3, 2.1, 1.1, 5.2, 3.1])
rounded = np.around(arr) # Are you sure you don't want to use np.floor?
unique_elems, counts = np.unique(rounded, return_counts=True)
out = arr[ np.isin(rounded, unique_elems[counts >= 3]) ]
out:
array([2.2, 2.3, 5.1, 3.2, 5.3, 3.3, 2.1, 5.2, 3.1])
