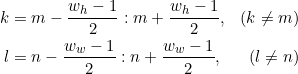Vectorizing a function for finding local minima and maxima in a 2D array with strict comparison-CodePudding

I'm trying to improve the performance of a function that returns the local minima and maxima of an input 2D NumPy array. The function works as expected, but it is too slow for my use case. I'm wondering if it's possible to create a vectorized version of this function to improve its performance.

Here is the formal definition for defining whether an element is a local minima (maxima):

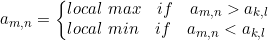
where

A=[a_m,n] is the 2D matrix, m and n are the row and column respectively, w_h and w_w are the height and width of the sliding windows, respectively.

I have tried using skimage.morphology.local_minimum and skimage.morphology.local_maxima, but they consider an element a minimum (maximum) if its value is less than or equal to (greater than or equal to) all of its neighbors.
In my case, I need the function to consider an element a minimum (maximum) if it is strictly less than (greater than) all of its neighbors.

The current implementation uses a sliding window approach with numpy.lib.stride_tricks.sliding_window_view, but the function does not necessarily have to use this approach.

Here is my current implementation:

import numpy as np

def get_local_extrema(array, window_size=(3, 3)):
    # Check if the window size is valid
    if not all(size % 2 == 1 and size >= 3 for size in window_size):
        raise ValueError("Window size must be odd and >= 3 in both dimensions.")

    # Create a map to store the local minima and maxima
    minima_map = np.zeros_like(array)
    maxima_map = np.zeros_like(array)

    # Save the shape and dtype of the original array for later
    original_size = array.shape
    original_dtype = array.dtype
    # Get the halved window size
    half_window_size = tuple(size // 2 for size in window_size)

    # Pad the array with NaN values to handle the edge cases
    padded_array = np.pad(array.astype(float),
                         tuple((size, size) for size in half_window_size),
                         mode='constant', constant_values=np.nan)

    # Generate all the sliding windows
    windows = np.lib.stride_tricks.sliding_window_view(padded_array, window_size).reshape(
        original_size[0] * original_size[1], *window_size)

    # Create a mask to ignore the central element of the window
    mask = np.ones(window_size, dtype=bool)
    mask[half_window_size] = False

    # Iterate through all the windows
    for i in range(windows.shape[0]):
        window = windows[i]
        # Get the value of the central element
        center_val = window[half_window_size]
        # Apply the mask to ignore the central element
        masked_window = window[mask]

        # Get the row and column indices of the central element
        row = i // original_size[1]
        col = i % original_size[1]

        # Check if the central element is a local minimum or maximum
        if center_val > np.nanmax(masked_window):
            maxima_map[row, col] = center_val
        elif center_val < np.nanmin(masked_window):
            minima_map[row, col] = center_val

    return minima_map.astype(original_dtype), maxima_map.astype(original_dtype)

a = np.array([[8, 8, 4, 1, 5, 2, 6, 3],
              [6, 3, 2, 3, 7, 3, 9, 3],
              [7, 8, 3, 2, 1, 4, 3, 7],
              [4, 1, 2, 4, 3, 5, 7, 8],
              [6, 4, 2, 1, 2, 5, 3, 4],
              [1, 3, 7, 9, 9, 8, 7, 8],
              [9, 2, 6, 7, 6, 8, 7, 7],
              [8, 2, 1, 9, 7, 9, 1, 1]])

(minima, maxima) = get_local_extrema(a)

print(minima)
# [[0 0 0 1 0 2 0 0]
#  [0 0 0 0 0 0 0 0]
#  [0 0 0 0 1 0 0 0]
#  [0 1 0 0 0 0 0 0]
#  [0 0 0 1 0 0 3 0]
#  [1 0 0 0 0 0 0 0]
#  [0 0 0 0 6 0 0 0]
#  [0 0 1 0 0 0 0 0]]

print(maxima)
# [[0 0 0 0 0 0 0 0]
#  [0 0 0 0 7 0 9 0]
#  [0 8 0 0 0 0 0 0]
#  [0 0 0 4 0 0 0 8]
#  [6 0 0 0 0 0 0 0]
#  [0 0 0 0 0 0 0 8]
#  [9 0 0 0 0 0 0 0]
#  [0 0 0 9 0 9 0 0]]

expected_minima = np.array([[0, 0, 0, 1, 0, 2, 0, 0],
                            [0, 0, 0, 0, 0, 0, 0, 0],
                            [0, 0, 0, 0, 1, 0, 0, 0],
                            [0, 1, 0, 0, 0, 0, 0, 0],
                            [0, 0, 0, 1, 0, 0, 3, 0],
                            [1, 0, 0, 0, 0, 0, 0, 0],
                            [0, 0, 0, 0, 6, 0, 0, 0],
                            [0, 0, 1, 0, 0, 0, 0, 0]])

expected_maxima = np.array([[0, 0, 0, 0, 0, 0, 0, 0],
                            [0, 0, 0, 0, 7, 0, 9, 0],
                            [0, 8, 0, 0, 0, 0, 0, 0],
                            [0, 0, 0, 4, 0, 0, 0, 8],
                            [6, 0, 0, 0, 0, 0, 0, 0],
                            [0, 0, 0, 0, 0, 0, 0, 8],
                            [9, 0, 0, 0, 0, 0, 0, 0],
                            [0, 0, 0, 9, 0, 9, 0, 0]])

np.testing.assert_array_equal(minima, expected_minima)
np.testing.assert_array_equal(maxima, expected_maxima)

print('All tests passed')

Any suggestions or ideas on how to vectorize this function would be greatly appreciated.

Thanks in advance!

EDIT #1
After playing a bit with NumPy, I managed to get the following code to almost work, in a completely vectorized way if I understood correctly:

def get_local_extrema_2(img):
  minima_map = np.zeros_like(img)
  maxima_map = np.zeros_like(img)

  minima_map[1:-1, 1:-1] = np.where(
    (a[1:-1, 1:-1] < a[:-2, 1:-1]) &
    (a[1:-1, 1:-1] < a[2:, 1:-1]) &
    (a[1:-1, 1:-1] < a[1:-1, :-2]) &
    (a[1:-1, 1:-1] < a[1:-1, 2:]) &
    (a[1:-1, 1:-1] < a[2:, 2:]) &
    (a[1:-1, 1:-1] < a[:-2, :-2]) &
    (a[1:-1, 1:-1] < a[2:, :-2]) &
    (a[1:-1, 1:-1] < a[:-2, 2:]),
    a[1:-1, 1:-1],
    0)
  
  maxima_map[1:-1, 1:-1] = np.where(
    (a[1:-1, 1:-1] > a[:-2, 1:-1]) &
    (a[1:-1, 1:-1] > a[2:, 1:-1]) &
    (a[1:-1, 1:-1] > a[1:-1, :-2]) &
    (a[1:-1, 1:-1] > a[1:-1, 2:]) &
    (a[1:-1, 1:-1] > a[2:, 2:]) &
    (a[1:-1, 1:-1] > a[:-2, :-2]) &
    (a[1:-1, 1:-1] > a[2:, :-2]) &
    (a[1:-1, 1:-1] > a[:-2, 2:]),
    a[1:-1, 1:-1],
    0)

  return minima_map, maxima_map

Output of get_local_extrema_2 is:
Minima map:

[[0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0]
 [0 0 0 0 1 0 0 0]
 [0 1 0 0 0 0 0 0]
 [0 0 0 1 0 0 3 0]
 [0 0 0 0 0 0 0 0]
 [0 0 0 0 6 0 0 0]
 [0 0 0 0 0 0 0 0]]

Maxima map:

[[0 0 0 0 0 0 0 0]
 [0 0 0 0 7 0 9 0]
 [0 8 0 0 0 0 0 0]
 [0 0 0 4 0 0 0 0]
 [0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0]]

The problem with the above is that pixels on the border that are minima or maxima are not detected.

EDIT #2
It would be fine even if in the output arrays there is 1 instead of the value of the local minima (maxima) i.e. a 2d array of 0 and 1 (or False and True).

EDIT #3
Here is a version of the function based on Cris Luengo's answer. Notice the use of the mode 'mirror' (equivalent to NumPy 'reflect') so that if a minima or maxima is on the edge, it will not be copied outside the border and it will stand out. This way, there is no need to pad the image with the minimum or maximum element of the matrix. I think this is the most performant way to accomplish this task:

import numpy as np
import scipy

def get_local_extrema_v3(image):
    footprint = np.ones((3, 3), dtype=bool)
    footprint[1, 1] = False
    minima = image * (scipy.ndimage.grey_erosion(image, footprint=footprint, mode='mirror') > image)
    maxima = image * (scipy.ndimage.grey_dilation(image, footprint=footprint, mode='mirror') < image)
    return minima, maxima

CodePudding user response：

Your definition of local maximum is flawed. For example, in a 1D array [1,2,3,4,4,3,2,1], there is a local maximum, but your definition ignores it. skimage.morphology.local_maxima will correctly identify this local maximum.

If you really need to implement your definition, I would use a dilation (erosion) with a square structuring element of the window size, but excluding the central pixel. Any pixel that is larger (smaller) in the original image than in the filtered image will satisfy your definition of local maximum (minimum).

I implemented this using scikit-image, but discovered it does a weird thing at the image edge, so it will not detect local maxima or minima near the edge:

se = np.ones((3, 3))
se[1, 1] = 0
minima = a * (skimage.morphology.erosion(a, footprint=se) > a)
maxima = a * (skimage.morphology.dilation(a, footprint=se) < a)

Using DIPlib (disclosure: I'm an author) this will work correctly also at the image edge:

import diplib as dip

se = np.ones((3, 3), dtype=np.bool_)
se[1, 1] = False
minima = a * (dip.Erosion(a, se) > a)
maxima = a * (dip.Dilation(a, se) < a)

^{Looking at the source code for skimage.morphology.dilation, it calls scipy.ndimage.grey_dilation with the default boundary extension, which is 'reflect'. This means that every local maximum at the image edge will have a neighbor with the same value, and hence not detected as local maximum in this definition. Instead, it should use the 'constant' extension, with cval set to the minimum possible value for the data type. For example, for an uint8 input array, it should do ndi.grey_dilation(image, footprint=footprint, output=out, mode='constant', cval=0). GitHub issue}