Gekko model with variable delay-CodePudding

I have a system with a non-constant delay. Does gekko support this type of problem and can it be handled in the MHE and MPC formulation?

Reading the docs I can see how to implement the delay, but I am not sure how the state estimation part of the MPC/MHE will handle this or if it is even capable to deal with such problems.

CodePudding user response：

There is no problem to include variable time delay in estimation or control problems. There is a reformulation of the problem to allow for continuous 1st and 2nd derivatives that are needed for a gradient-based optimizer. I recommend that you use a cubic spline to create a continuous approximation of the discontinuous delay function. This way, the delay can be fractional such as theta=2.3. If the delay must be integer steps then set integer=True for the theta decision variable.

theta_ub = 30 # upper bound to dead-time
theta = m.FV(0,lb=0,ub=theta_ub); theta.STATUS=1

# add extrapolation points
td = np.concatenate((np.linspace(-theta_ub,min(t)-1e-5,5),t))
ud = np.concatenate((u[0]*np.ones(5),u))
# create cubic spline with t versus u
uc = m.Var(u); tc = m.Var(t); m.Equation(tc==time-theta)
m.cspline(tc,uc,td,ud,bound_x=False)

Here is an example of one cycle of Moving Horizon Estimation with a first-order plus dead-time (FOPDT) model with variable time delay. This example is from the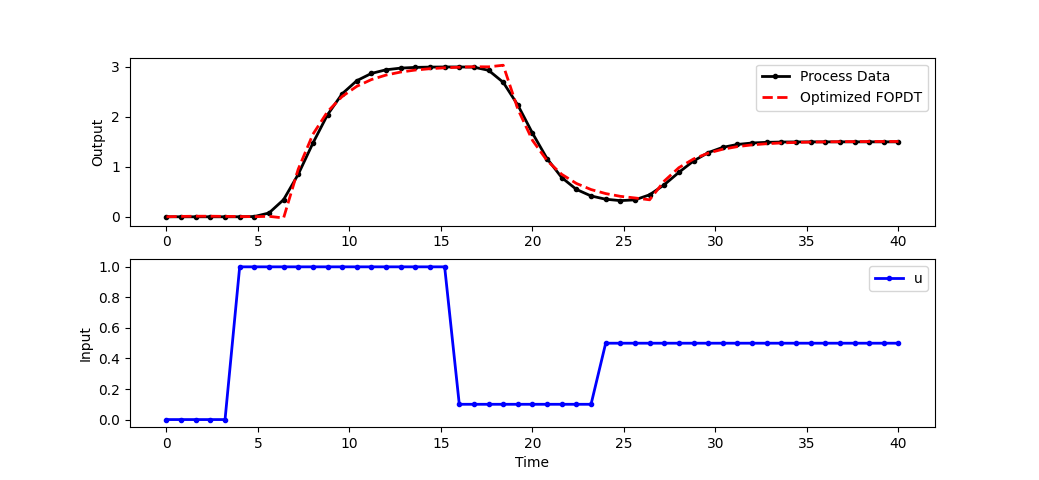

import numpy as np
import pandas as pd
from gekko import GEKKO
import matplotlib.pyplot as plt

# Import CSV data file
# Column 1 = time (t)
# Column 2 = input (u)
# Column 3 = output (yp)
url = 'http://apmonitor.com/pdc/uploads/Main/data_fopdt.txt'
data = pd.read_csv(url)
t = data['time'].values - data['time'].values[0]
u = data['u'].values
y = data['y'].values

m = GEKKO(remote=False)
m.time = t; time = m.Var(0); m.Equation(time.dt()==1)

K = m.FV(2,lb=0,ub=10);      K.STATUS=1
tau = m.FV(3,lb=1,ub=200);  tau.STATUS=1
theta_ub = 30 # upper bound to dead-time
theta = m.FV(0,lb=0,ub=theta_ub); theta.STATUS=1

# add extrapolation points
td = np.concatenate((np.linspace(-theta_ub,min(t)-1e-5,5),t))
ud = np.concatenate((u[0]*np.ones(5),u))
# create cubic spline with t versus u
uc = m.Var(u); tc = m.Var(t); m.Equation(tc==time-theta)
m.cspline(tc,uc,td,ud,bound_x=False)

ym = m.Param(y); yp = m.Var(y)
m.Equation(tau*yp.dt() (yp-y[0])==K*(uc-u[0]))

m.Minimize((yp-ym)**2)

m.options.IMODE=5
m.solve()

print('Kp: ', K.value[0])
print('taup: ',  tau.value[0])
print('thetap: ', theta.value[0])

# plot results
plt.figure()
plt.subplot(2,1,1)
plt.plot(t,y,'k.-',lw=2,label='Process Data')
plt.plot(t,yp.value,'r--',lw=2,label='Optimized FOPDT')
plt.ylabel('Output')
plt.legend()
plt.subplot(2,1,2)
plt.plot(t,u,'b.-',lw=2,label='u')
plt.legend()
plt.ylabel('Input')
plt.xlabel('Time')
plt.show()