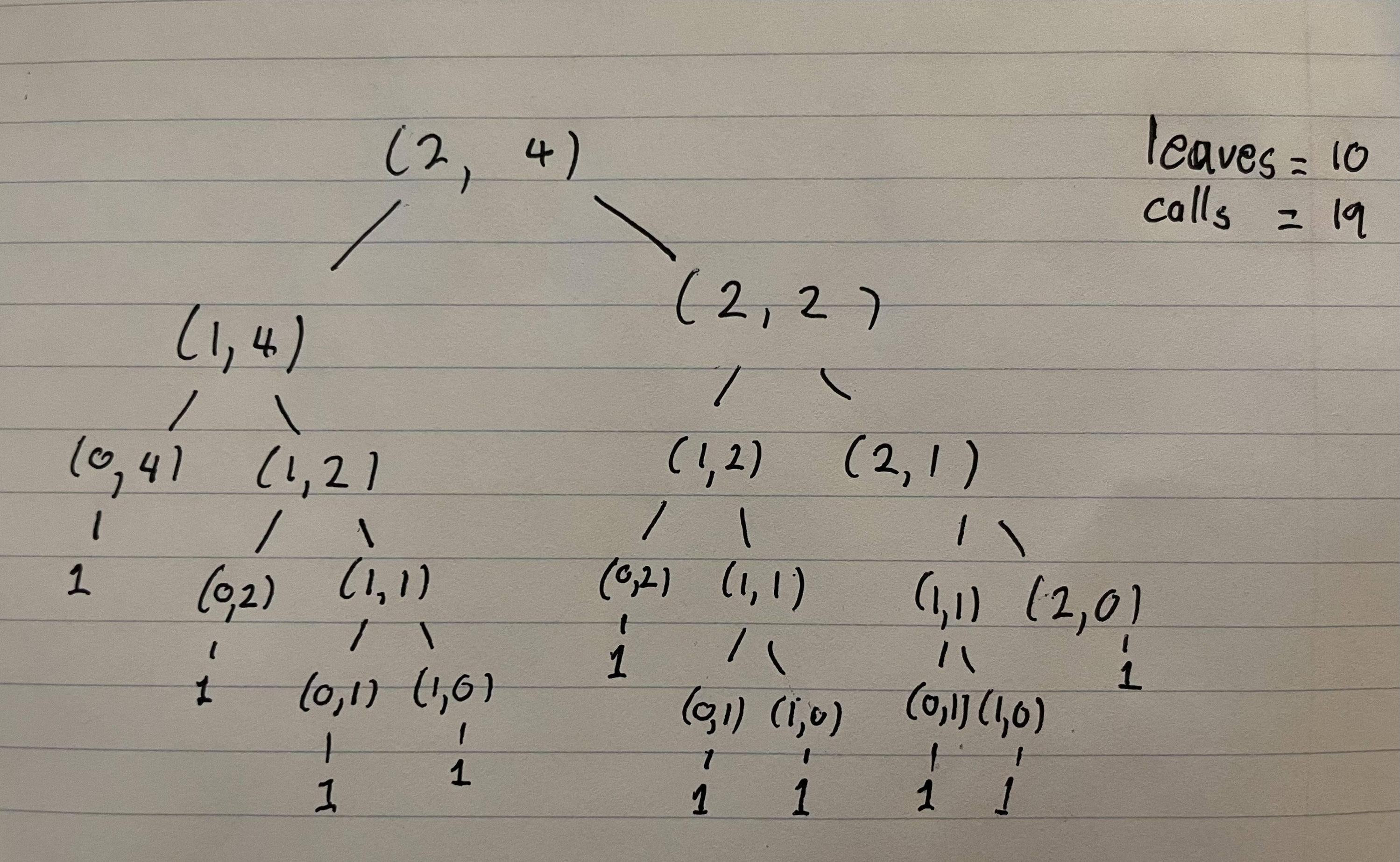I'm not sure how the two recursive calls and the floor division of the following function interact regarding time complexity and big o notation.

def recurse(n: int, k: int) -> int:
    if n <= 0 or k <= 0:
        return 1
    return recurse(n//2, k)   recurse(n, k//2)

I see how O(2^(nk)) could serve as an upper bound because the k portion of (n//2,k) and the n portion of (n,k//2) dominate the growth rates. However I could also see something along the lines of (nlog(n)*mlog(m)) working as well and I'm not sure what to settle on.

Edit:

CodePudding user response：

Each call itself only does constant work, so overall time is proportional to the number of calls.

Let N and K be the arguments to the top call. Recursive calls keep one argument and halve the other. The first argument can get halved at most log2(N) times and the second argument at most log2(K) times. So you can't recurse deeper than log2(N) log2(K) times. Thus we have at most 2^{log2(N) log2(K) 1}-1 = 2•2^log2(NK)-1 = 2NK-1 calls. So complexity is O(NK).

Some testing suggests it's even less, i.e., O(NK) isn't tight. For N=K, it looks like O(NK / sqrt(log2(NK))).

CodePudding user response：

Here's an exact solution.

The first thing to note is that, ignoring cases where n < 0 or k < 0, we only care about how many times we need to divide n or k by two (using floor division) before they reach zero. For example, if n = 7, then we have 7, 3, 1, 0, which is three divisions by two.

The number of times a non-negative integer v can be divided by two (using floor division) before reaching zero is ceil(log2(v 1)).

Let a = ceil(log2(n 1)) and b = ceil(log2(k 1)). Then each recursive call reduces either a or b by one, and continues until either a or b reaches zero.

Now consider the call tree. This is a binary tree, but not a balanced tree (since some paths are longer than others). A call is a leaf call if either n or k is zero. Further, each leaf call corresponds to a single unique path through the call tree. Each recursive call reduces either a or b by one, so each leaf call corresponds to a unique monotonic path from (a, b) to either (0, x) or (x, 0), since the recursive calls end when either a or b becomes zero. We can model this by extending each path to (0, 0). Then we just need to count the number of paths from (a, b) to (0, 0). This is just (a b)!/(a!*b!).

This is a well-known result that isn't difficult to derive. It can be expressed as a multicombination (i.e., a combination in which multiple instances of a given value are allowed).

So the number of leaf calls is (a b)!/(a!*b!). The number of non-leaf calls is one less than this. So we have:

1. leaf calls: (a b)!/(a!*b!)
2. non-leaf calls: (a b)!/(a!*b!) - 1
3. total calls: 2*(a b)!/(a!*b!) - 1

The exact time complexity of recurse is O((a b)!/(a!*b!)), where a = ceil(log2(n 1)) and b = ceil(log2(k 1)).

The return value of recurse is the number of leaf calls. The function complexity below behaves identically:

from math import factorial

def complexity(n: int, k: int) -> int:
    if n <= 0 or k <= 0:
        return 1

    a = ceil_log2(n 1)
    b = ceil_log2(k 1)

    return factorial(a   b) // (factorial(a) * factorial(b))

where ceil_log2 is defined as:

def ceil_log2(x):
    if x <= 0:
        raise ValueError("log2 of zero or negative integer")

    return (x - 1).bit_length()