How to get all leaf nodes from a directed subtree using igraph in R?-CodePudding

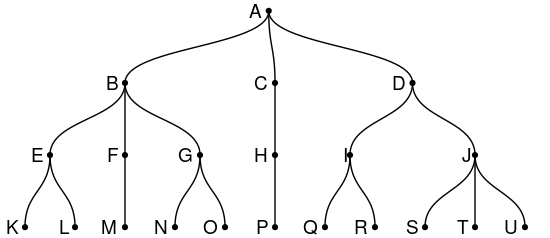
Given is a tree (igraph graph) constructed from a dataframe:

library(igraph)
library(ggraph)

#Create a symbolic edge list.
edgelist_df <- data.frame("from" = c("A", "A", "A", "B", "B", "B", "C", "D", "D", "E", 
                                     "E", "F", "G", "G", "H", "I", "I", "J", "J", "J"),
                          "to"   = c("B", "C", "D", "E", "F", "G", "H", "I", "J", "K", 
                                     "L", "M", "N", "O", "P", "Q", "R", "S", "T", "U"))

Then create a directed graph/tree from this edgelist (edgelist_df)

graph <- graph_from_data_frame(d = edgelist_df, directed = TRUE)

Plot the tree. Here I'm using package ggraph with function ggraph.

ggraph(graph = graph, 
       layout = 'dendrogram', 
       circular = FALSE)  
  geom_edge_diagonal()  
  geom_node_point()  
  geom_node_text(aes(label = name),
                 angle = 0,
                 hjust = 1.5,
                 nudge_y = 0,
                 size = 5)  
  theme_void()

The question is how to return a character vector containing the names of all leaf nodes from a subtree that is specified by one node, representing the root node of that subtree. For example:

If node = "B", then all leaf nodes that are part of the subtree with root "B" are: "K", "L", "M", "N" and "O".
If node = "H", then all leaf nodes that are part of the subtree with root "H" are: "P".
If node = "A", then all leaf nodes that are part of the subtree with root "A" (which is the original tree) are: "K", "L", "M", "N", "O", "P", "Q", "R", "S", "T" and "U".

CodePudding user response：

Assuming that object graph is indeed a tree, then the function below gives the desired result.

determine_leaf_nodes_subtree <- function(graph, vertex){

#Determine the name of the root vertex.
root               <- V(graph)$name[degree(graph = graph, v = V(graph), mode = "in") == 0]

#Determine the name(s) of the leaf vertex/vertices.
leafs              <- V(graph)$name[degree(graph = graph, v = V(graph), mode = "out") == 0]

#Calculate the tree depth. That is, the smallest path length of all shortest paths from root 
#to leaf vertices.
sh_paths           <- shortest_paths(graph = graph, from = root, to = leafs)$vpath 
max_sh_path_length <- max(sapply(X = sh_paths, FUN = length))

#If 'vertex' is a leaf node itself, then return the name of that vertex.
if(vertex %in% leafs){

  return(vertex)

} else {
  
  #If 'vertex' is not a leaf node, then determine the subset of all vertices that are in the 
  #neighborhood of 'vertex', excluding 'vertex' itself ('mindist' = 1). The maximum order or 
  #'depth' is specified by ('max_sh_path_length')
  vertices_subset <- neighborhood(graph = graph, 
                                  order = max_sh_path_length - 1, 
                                  nodes = V(graph)[V(graph)$name == vertex], 
                                  mode = "out",
                                  mindist = 1)
  
  #Extract the names of the vertices in 'vertices_subset'
  vertices_subset_names <- names(unlist(vertices_subset))
  
  #The overlap/intersection of vertex names between 'vertices_subset_names' and 'leafs' gives 
  #all leaf nodes that are part of the subtree with root vertex 'vertex'.
  result <- intersect(x = vertices_subset_names, leafs)

  return(result)
 }
}

With respect to the examples stated in the question, this function gives the following output:

determine_leaf_nodes_subtree(graph = graph, vertex = "B")
[1] "K" "L" "M" "N" "O"

determine_leaf_nodes_subtree(graph = graph, vertex = "H")
[1] "P"

determine_leaf_nodes_subtree(graph = graph, vertex = "A")
[1] "K" "L" "M" "N" "O" "P" "Q" "R" "S" "T" "U"

CodePudding user response：

You can make two calls to ego: the first to grab all the nodes that can be reached from parent to child (mode="out"), and the second to see if these selected nodes have any children (if not then they are leaf nodes.

fun <- function(graph, node="B"){
  path <- ego(graph, order=length(V(graph)), nodes=node, mode="out")
  nms <- names(path[[1]])
  nms[ego_size(graph, order=1, nodes=nms, mode="out", mindist=1) == 0]
}

This produces

fun(graph, "B")
# [1] "K" "L" "M" "N" "O"
fun(graph, "H")
# [1] "P"
fun(graph, "A")
# [1] "K" "L" "M" "N" "O" "P" "Q" "R" "S" "T" "U"

In fact, taking a lead from Peters answer the call to ego_size could be replaced with

nms[degree(graph, v=nms, mode="out") == 0]

CodePudding user response：

You can define a function f with distances() and degree like below

f <- function(g, r) {
  names(V(g))[is.finite(distances(g, r, mode = "out")) & degree(g) == 1]
}

which gives

> f(g, "B")
[1] "K" "L" "M" "N" "O"