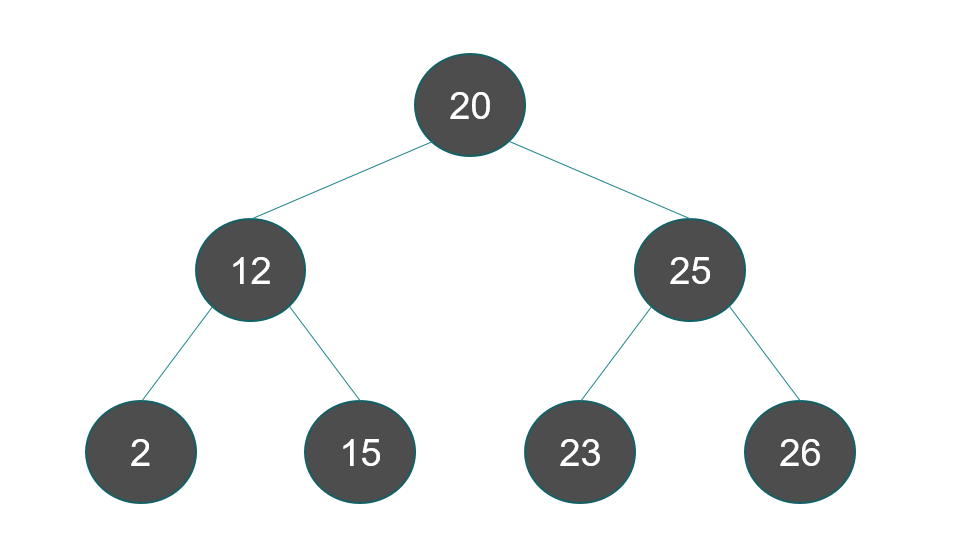
Properties of Red-Black Tree:
- Every node is either red or black.
- The root is black.
- Every leaf (NIL) is black.
- If a node is red, then both its children are black.
- For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
According to the properties, are these valid or invalid red black trees?
I think this is valid
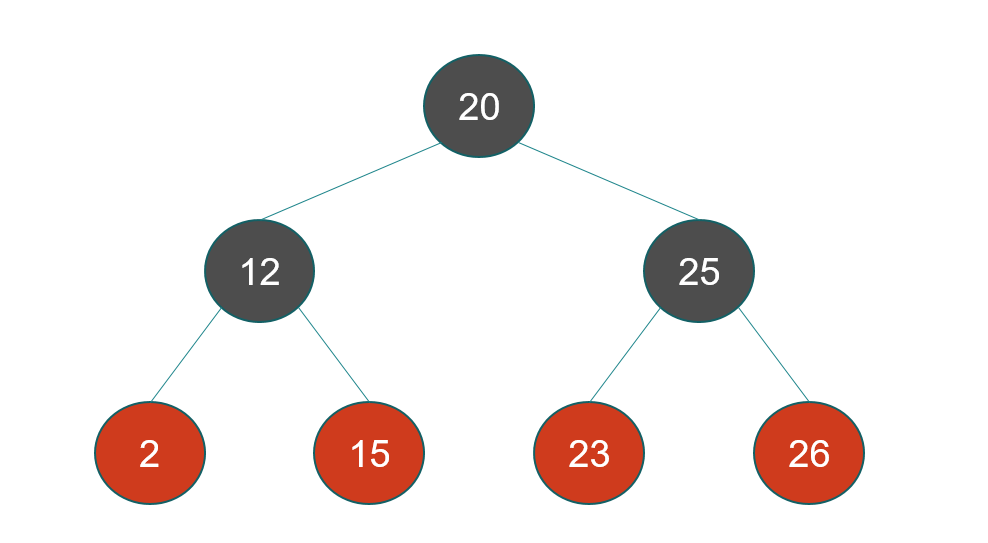
I think this is valid, but I am not sure since there two adjacent red nodes?
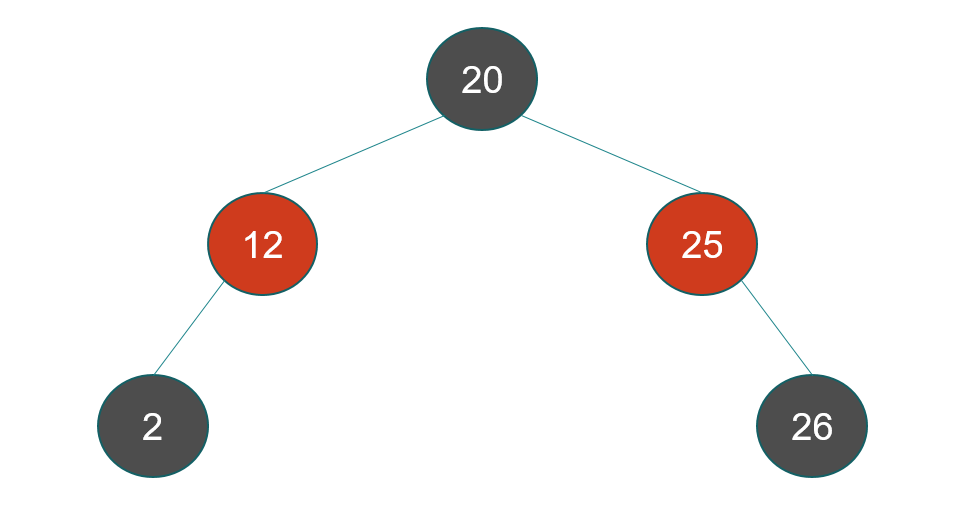
I think this is valid, but I am not sure since there two adjacent red nodes?
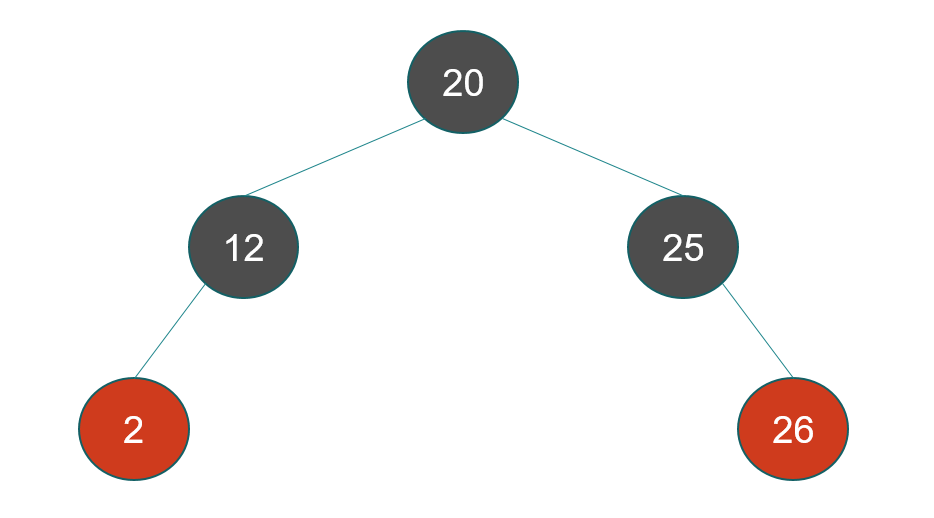
I think this is not valid since it violate Property 4?
Did I understand these properties of a RBtree right? If not, where am I wrong?
CodePudding user response:
A, B & D are valid red-black trees
C is not valid red-black tree as the black height from root to leaf is not the same. It is 2 in some paths and 1 in other paths. It violates what you stated as rule 5.
If 12 had a right child that was black and 25 a left child that was black, then it would be a red-black tree.
CodePudding user response:
You have listed the properties of Red-Black trees correctly. Of the four trees only C is not a valid red-black tree:
I think this is valid, but I am not sure since there two adjacent red nodes?
It is valid. There is no problem with red nodes being siblings. They just should not be in a parent-child relationship.
I think this is valid, but I am not sure since there two adjacent red nodes?
It is not valid. Not because of the adjacent red nodes, but because of property 5. The node with label 12 has paths to its leaves with varying number of black nodes. Same for the node 25.
As a general rule, a red node can never have exactly one NIL-leaf as child. Its children should either both be NIL-leaves, or both be (black) internal nodes. This follows from the properties.
I think this is not valid since it violate Property 4?
Property 4 is not violated: the children of the red nodes are NIL leaves (not visualised here), which are black. The fact that these red nodes have black NIL leaves as siblings is irrelevant: there are no rules that concern siblings. So this is valid.
For an example that combines characteristics of tree C and D, see this valid tree depicted in the