I am trying to find the vector or angle in order to calculate the points where two "thick" lines would intersect. The end goal is to draw simple flat planes for a thick line renderer.
Although I'm using Unity and am working with Vector3, for my purposes, assume the Z-value is always 0. This is a 2d problem. It is not a Unity specific problem and I'm not sure why I'm having a hard time finding a solution that I can understand. Getting points for drawing a "thick" line is surely not new. But for the life of me, I can't find a solution.
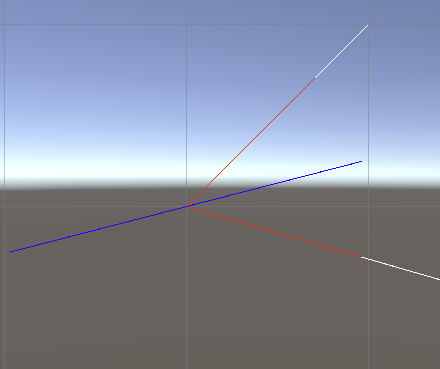
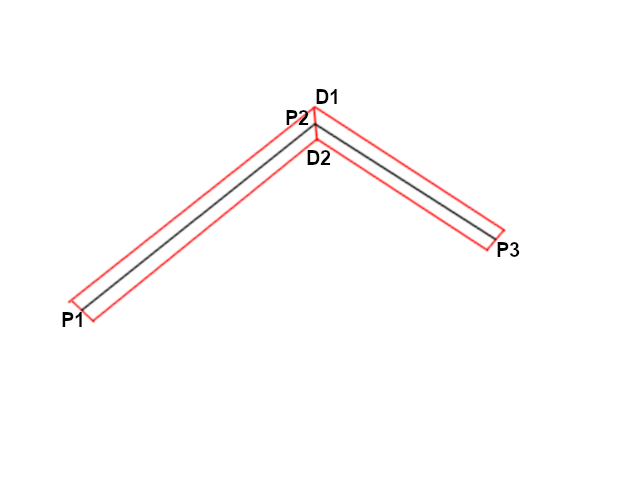
The closest I've come is figuring out points along the line perpendicular to the one I want. I know that this is the "bounce" line. In other words, with 3 points, I can get the vector for the line that represents the side of a billiard ball table assuming the middle point is the point of impact with the side of the table. What I want is the vector perpendicular to that side. I worked out the code below according to the post here: 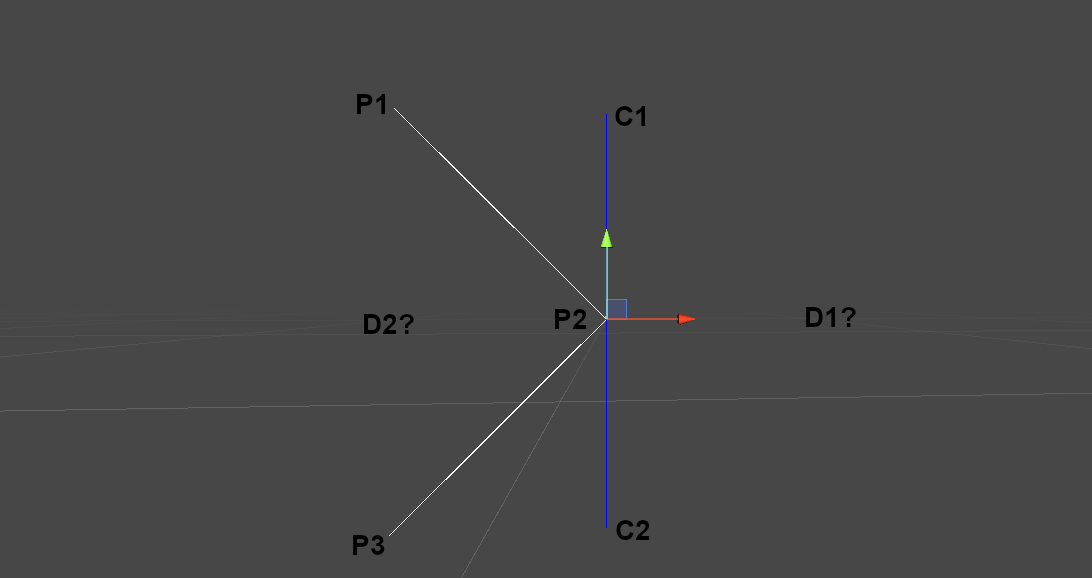
CodePudding user response:
Not 100% sure of the intended logic here, but the part that seems screwy to me in your code is this bit:
Vector3 n1 = (p2 - p1).normalized;
Vector3 n2 = (p3 - p2).normalized;
Here, you're getting a normal of one line and the inverted normal of the other line, which you later add together. This leads to the "bounce wall" line you described because you're mirroring one normal across the intersection point. Don't you mean:
Vector3 n1 = (p3 - p2).normalized;
Vector3 n2 = (p1 - p2).normalized;
When you make the signs the same by fixing that issue, both normals are on one side of the intersection point. Adding them together then leads to y-components that somewhat cancel each other out, and an x-component on the correct side of the intersection point. The drawn blue line then takes the angle you want it to (fixed normals in red):
Full modified version of your code I used to make this:
using UnityEngine;
public class ThickLineRenderer : MonoBehaviour {
public Vector3 line1Start = new Vector3(-1, -1);
public Vector3 intersect = new Vector3(0, 0);
public Vector3 line2Start = new Vector3(-1, 1);
private void OnDrawGizmos() {
Vector3[] points = new Vector3[] { line1Start, intersect, line2Start };
Vector3 p1 = points[0];
Vector3 p2 = points[1];
Vector3 p3 = points[2];
Gizmos.color = Color.white;
Gizmos.DrawLine(p1, p2);
Gizmos.DrawLine(p2, p3);
Vector3 n1 = (p3 - p2).normalized;
Vector3 n2 = (p1 - p2).normalized;
Gizmos.color = Color.red;
Gizmos.DrawLine(p2, n1);
Gizmos.DrawLine(p2, n2);
Vector3 n = (n1 n2).normalized;
Vector3 d = p2 n;
Vector3 d2 = p2 - n;
Gizmos.color = Color.blue;
Gizmos.DrawLine(p2, d);
Gizmos.DrawLine(p2, d2);
}
}
(Sorry I don't quite have the right vocabulary to describe this issue, it's been a long time since trigonometry. Hopefully this makes sense.)
CodePudding user response:
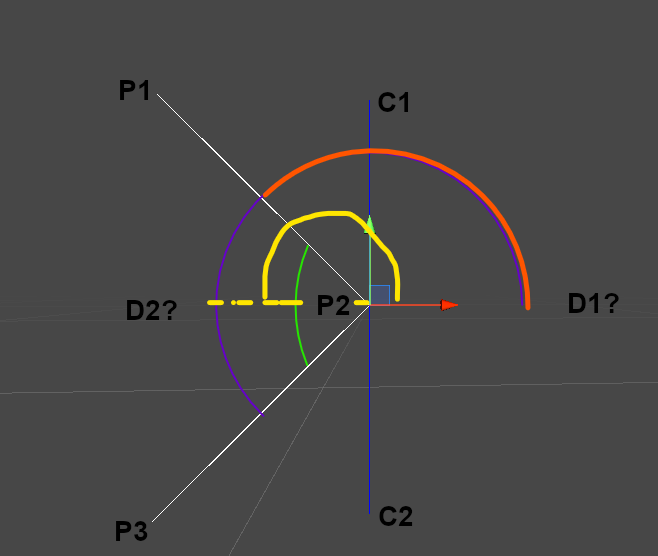
Hello I am not really sure if I reaaally understood what you were trying to accomplish but to me your problem looks like this you got three points P1,P2,P3 and you wish to find exactly the "normal angle" the yellow angle between the P12 and P23 lines.
One way to do this is to calculate the absolute angles this means the angle formed between the x axis and each line section.In the image bellow they are the orange and purple angles. Then the substraction will tell you the angle formed between P12 and P23 this is the green angle. Finally to obtain what i believe is what you call the "normal angle", which lies precisely at the middle of the green angle, you just need to subtract half of the green angle from the bigger angle in this case the purple one.
I made a simple Console program to make the calculations here'sthe code
using System;
namespace ConsoleApp1
{
class Program
{
public static double GetAbsAngle(double x, double y)
{
double radsAbsAngle;
//Get the absolute angle from respect to the x axis given a podouble x,y
if (y > 0)
{
radsAbsAngle = Math.Atan2(y, x);
return radsAbsAngle;
}
//Here Math.Atan2(y, x) will always result negative
radsAbsAngle = 2*Math.PI Math.Atan2(y, x);
return radsAbsAngle;
}
public static double AngleBetweenPoints(double x1, double y1, double x2, double y2)
{
double absAngleP1 = Program.GetAbsAngle(x1, y1);
Console.WriteLine("Abs angle P1 in degrees: {0}", Program.RadiansToDegrees(absAngleP1));
double absAngleP2 = Program.GetAbsAngle(x2, y2);
Console.WriteLine("Abs angle P2 in degrees: {0}", Program.RadiansToDegrees(absAngleP2));
double angleBetween;
angleBetween = (x1 > x2) ? absAngleP1 - absAngleP2 : absAngleP2 - absAngleP1;
return angleBetween;
}
public static double RadiansToDegrees(double radians)
{
double degrees = (180 / Math.PI) * radians;
return (degrees);
}
static void Main(string[] args)
{
//P1 with
double x1 = -4;
double y1 = 4;
//Assuming that P2 is always at 0,0
//P3 with
double x3 = -4;
double y3 = -4;
double angleBetween = Program.AngleBetweenPoints(x1, y1, x3, y3);
Console.WriteLine("Angle between P1 and P3 in degrees: {0}",Program.RadiansToDegrees(angleBetween));
double p1Angle = Program.GetAbsAngle(x1, y1);
double p3Angle = Program.GetAbsAngle(x3, y3);
double absNormalAngle = (p1Angle > p3Angle) ? p1Angle - (angleBetween/ 2) : p3Angle - (angleBetween / 2);
Console.WriteLine("The normal abs angle between P1 and P3 in degrees: {0}", Program.RadiansToDegrees(absNormalAngle));
}
}
}
The result is the following
Abs angle P1 in degrees: 135
Abs angle P2 in degrees: 225
Angle between P1 and P3 in degrees: 90
The normal abs angle between P1 and P3 in degrees: 180