Calculate area on 3D surface mesh encolosed by four arbitrary points from coordinate data-CodePudding

I have human facial data as below:

library(Rvcg)
library(rgl)

data(humface)

lm <- matrix(c(1.0456182e 001, -3.5877686e 001, 5.0972912e 001, 2.2514189e 001,
               8.4171227e 001, 6.6850304e 001, 8.3239525e 001, 9.8277359e 000,
               6.5489395e 001, 4.2590347e 001, 4.0016006e 001, 5.9176712e 001), 
              4)

shade3d(humface, col="#add9ec", specular = "#202020", alpha = 0.8)     
plot3d(lm, type = "s", col = "red", xlab = "x", ylab = "y", zlab = "z", 
       size = 1, aspect = FALSE,add=T)

for lm, four landmarks are placed on the surface of the mesh, in the following oder:

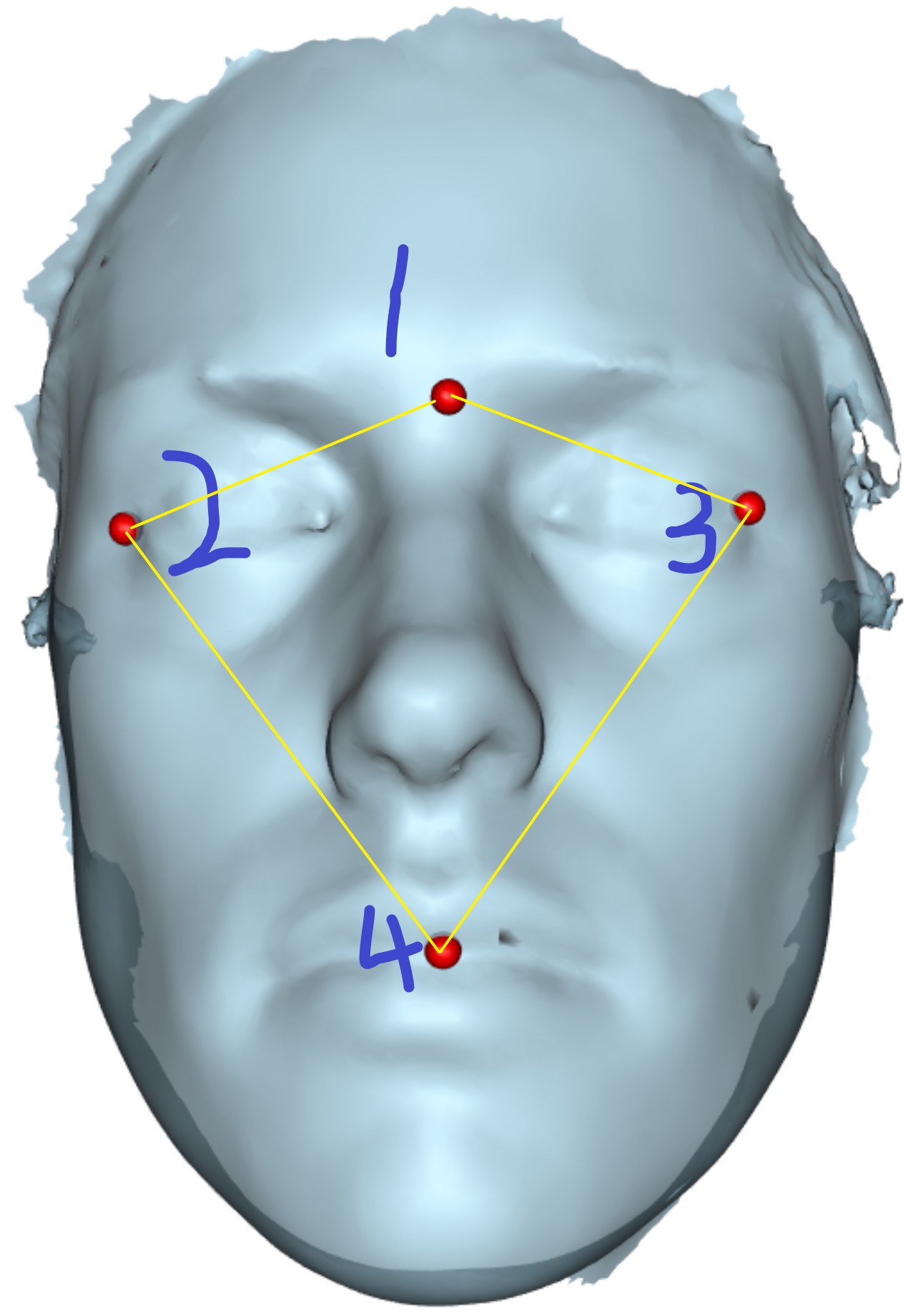
The yellow lines are drawn by hand for illustration purpose. I wish to calculate the surface area of the quarilateral enclosed by the four red dots, i.e., the surface area inside the yellow edges.

If surface area cannot be calculated, I also welcome methods to calculate the area (not area of the surface of the face) of the quadrilateral. I know one could calculate the sum of areas of triangle 123 and triangle 234. However, I my real application, I have no idea of the ordering and relative spatial position of the four points. Since I have thousands of qudrilateral areas to calculate, it is impossible to plot each quadrilateral and determine how to decompose the quadrilateral into two triangles. For example, I may accidentally pick triangle 123 and triangle 124, and the sum of these two triangle ares is not what I want.

Therefore, I am interested in either surface area or area of the quadrilateral. Solution to either is welcome. I just do not want to plot each quadrilateral and I want an area value directly computed from the coordinates.

CodePudding user response：

I believe your question is more appropriate for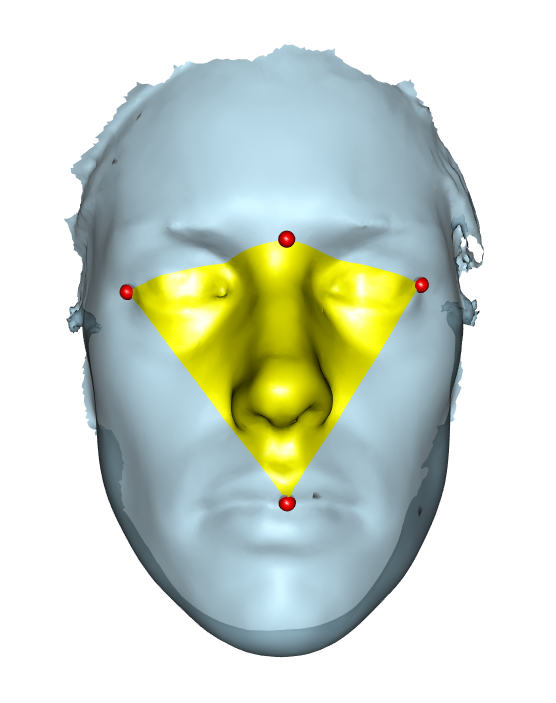

The projection ends up containing 3604 triangles; the area is

vcgArea(projection)
# [1] 5141.33

There are a few ambiguities in the problem: the quadrilateral isn't planar, so you'd get a different one if you split it into triangles along the other diagonal. And the projection of the quad onto the face is different depending on which direction you choose. I used the default of projecting along the z axis, but in fact the face isn't perfectly aligned that way.