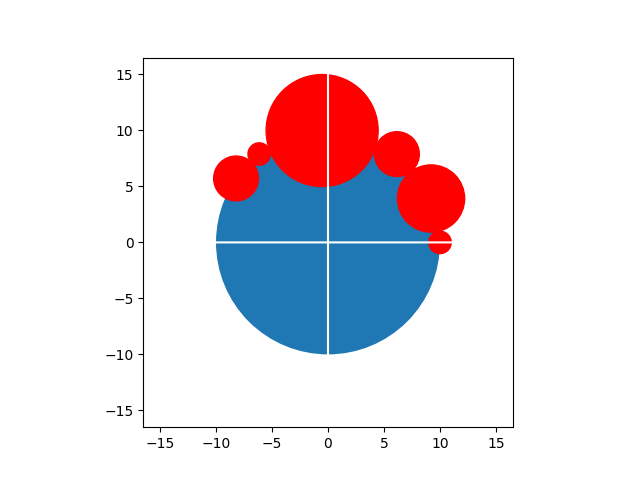
I'd like to position a set of circles along another circle in such a way that "child" circles do not overlap with each other. I know the radius of all the circles, as well as the position of the target circle.

The target circle will always be large enough to fit all the circles.

See this diagram:

:

interface Circle {
  radius: number;
  x: number;
  y: number;
}

const childRadii = [1, 3, 2, 5, 1, 2];

const largeCircle = { radius: 10, x: 0, y: 0 };

const arrangedCircles = positionCirclesOnCircle(largeCircle, childRadii);

function positionCirclesOnCircle(
  largeCircle: Circle,
  radii: number[]
): Circle[] {
  const arrangedCircles: Circle[] = [];
  //for each of our radii  find the correct x and y position along largeCircle
  for (let index = 0; index < radii.length; index  ) {
    //find the x and y pos for this circle
    //push to arrangedCircles
  }
  return arrangedCircles;
}

I'm not sure what kind of equations or math I should to find the x and y positions for each of the child circles.

I see

About fitting:

1. It is impossible to put two adjacent circles if sum of their radiuses i greater than diameter of big circle.
2. The value of f[i] > 2 * Pi means that no more non overlapping circles can be added.

CodePudding user response：

Here is an alternative way. I tried to avoid the use of the "computationally expensive" functions arcsin, sin and cos, replaced them by the use of the expensive function sqrt only, you can try to adapt the following code to your needs.

import math
import numpy as np

def initial_child_cetner(large_circle, argument):
    cos_arg = math.cos(math.pi * argument / 180)
    sin_arg = math.sin(math.pi * argument / 180)
    rotation = np.array([[ cos_arg, -sin_arg],
                         [ sin_arg,  cos_arg]])
    initial_center = large_circle['radius'] * np.array([1., 0.])
    return rotation.dot(initial_center)

def cos_sin_angle(large_radius, chord):
    cos_angle = 1 - ( chord )**2 / (2*large_radius**2)  
    sin_angle = math.sqrt(1 - cos_angle**2)
    return cos_angle, sin_angle

def next_child_center(large_circle_center, current_child_center, large_radius, chord):
    cos_a, sin_a = cos_sin_angle(large_radius, chord)
    rotation = np.array([[ cos_a,  sin_a],
                         [-sin_a,  cos_a]])
    child_center_next =  large_circle_center   rotation.dot(current_child_center - large_circle_center)
    return child_center_next

def chain_of_child_circles(large_circle, child_radii, argument):
    n = len(child_radii)
    child_centers = np.empty((n, 2), dtype = float)
    child_centers[0, :] = initial_child_cetner(large_circle, argument)
    large_center = np.array([large_circle['x'], large_circle['y']])
    for i in range(n-1):
        chord = child_radii[i]   child_radii[i 1]
        child_centers[i 1, :] = next_child_center(large_center, 
                                                  child_centers[i, :], 
                                                  large_circle['radius'], 
                                                  chord) 
    return child_centers
    

childRadii = [1, 3, 2, 5, 1, 2]
largeCircle = { 'radius': 10, 'x': 0, 'y': 0 }

childCircleCenters = chain_of_child_circles(largeCircle, childRadii, -90)

fig, axs = plt.subplots()
axs.plot(childCircleCenters[:,0], childCircleCenters[:,1], 'bo')

axs.plot(childCircleCenters[:,0], childCircleCenters[:,1])


axs.set_aspect('equal')
plt.grid()
plt.show()