Endless sine generation in C-CodePudding

I am working on a project which incorporates computing a sine wave as input for a control loop. The sine wave has a frequency of 280Hz, the control loop runs every 30us and everything is written in C for an Arm Cortex M7. At the moment we are simply doing:

double time;
void control_loop() {
    time  = 30e-6;
    double sine = sin(2 * M_PI * 280 * time);
    ...
}

Two problems/questions arise:

When running for a long time, time becomes bigger. Suddenly there is a point where the computation time for the sine function increases drastically (see image). Why is this? How are these functions usually implemented? Is there a way to circumvent this (without noticable precision loss) as speed is a huge factor for us? We are using sin from math.h (Arm GCC).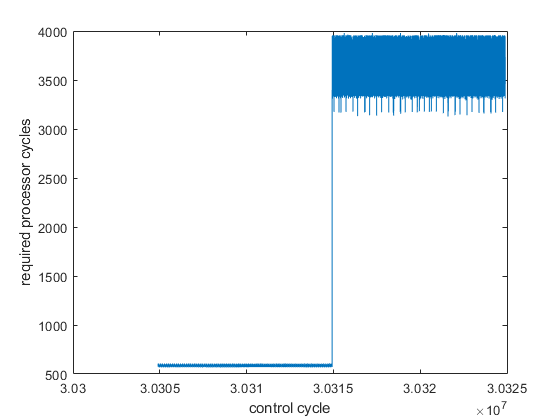
How to deal with time in general: When running for a long time, the variable time will inevitably reach the limits of double precision. Even using a counter time = counter * 30e-6; only improves this, but does not solve it. As I am certainly not the first person who wants to generate a sine wave for a long time, there must be some ideas/papers/... on how to implement this fast and precise.

CodePudding user response：

Instead of calculating sine as a function of time, maintain a sine/cosine pair and advance it through complex number multiplication. This doesn't require any trigonometric functions, and only occasional re-normalization:

static const double dx = cos(2 * M_PI * 280 * 30e-6), dy = sin(2 * M_PI * 280 * 30e-6);
double x = 0, y = 1;
int counter = 0;

void control_loop() {
    double xx = dx*x - dy*y, yy = dx*y   dy*x;
    x = xx, y = yy;

    if((counter   & 0xffff) == 0) { // once in a while
        double d = 1/hypot(x,y);
        x *= d, y *= d;
    }

    double sine = y; // this is your sine
}

CodePudding user response：

How to generate a lovely sine.

DAC is 12bits so you have only 4096 levels. It makes no sense to send more than 4096 samples per period. In real life you will need much less samples to generate a good quality waveform.

Create C file with the lookup table (using your PC). Redirect the output to the file (https://helpdeskgeek.com/how-to/redirect-output-from-command-line-to-text-file/).

#define STEP   ((2*M_PI) / 4096.0)

int main(void)
{
    double alpha = 0;

    printf("#include <stdint.h>\nconst uint16_t sine[4096] = {\n");
    for(int x = 0; x < 4096 / 16; x  )
    {
        for(int y = 0; y < 16; y  )
        {
            printf("%d, ", (int)(4095 * (sin(alpha)   1.0) / 2.0));
            alpha  = STEP;
        }
        printf("\n");
    }
    printf("};\n");
}

https://godbolt.org/z/e899d98oW

Configure the timer to trigger the overflow 4096*280=1146880 times per second. Set the timer to generate the DAC trigger event. For 180MHz timer clock it will not be precise and the frequency will be 279.906449045Hz. If you need better precision change the number of samples to match your timer frequency or/and change the timer clock frequency (H7 timers can run up to 480MHz)
Configure DAC to use DMA and transfer the value from the lookup table created in the step 1 to the DAC on the trigger event.
Enjoy beautiful sine wave using your oscilloscope. Note that your microcontroller core will not be loaded at all. You will have it for other tasks. If you want to change the period simple reconfigure the timer. You can do it as many times per second as you wish. To reconfigure the timer use timer DMA burst mode - which will reload PSC & ARR registers on the upddate event automatically not disturbing the generated waveform.

I know it is advanced STM32 programming and it will require register level programming. I use it to generate complex waveforms in our devices.

It is the correct way of doing it. No control loops, no calculations, no core load.

CodePudding user response：

As noted in some of the comments, the time value is continually growing with time. This poses two problems:

The sin function likely has to perform a modulus internally to get the internal value into a supported range.
The resolution of time will become worse and worse as the value increases, due to adding on higher digits.

Making the following changes should improve the performance:

double time;
void control_loop() {
    time  = 30.0e-6;
    if((1.0/280.0) < time)
    {
        time -= 1.0/280.0;
    }
    
    double sine = sin(2 * M_PI * 280 * time);
    ...
}

Note that once this change is made, you will no longer have a time variable.

CodePudding user response：

Use a look-up table. Your comment in the discussion with Eugene Sh.:

A small deviation from the sine frequency (like 280.1Hz) would be ok.

In that case, with a control interval of 30 µs, if you have a table of 119 samples that you repeat over and over, you will get a sine wave of 280.112 Hz. Since you have a 12-bit DAC, you only need 119 * 2 = 238 bytes to store this, which easily fits into a Cortex M7's L1 cache.

CodePudding user response：

The function can be rewritten as

double n;
void control_loop() {
    n  = 1;
    double sine = sin(2 * M_PI * 280 * 30e-6 * n);
    ...
}

That does exactly the same thing as the code in the question, with exactly the same problems. But it can now be simplified:

280 * 30e-6 = 280 * 30 / 1000000 = 21 / 2500 = 8.4e-3

Which means that when n reaches 2500, you've output exactly 21 cycles of the sine wave. Which means that you can set n back to 0. The resulting code is:

int n;
void control_loop() {
    n  = 1;
    if (n == 2500)
        n = 0;
    double sine = sin(2 * M_PI * 8.4e-3 * n);
    ...
}

As long as your code can run for 21 cycles without problems, it'll run forever without problems.

CodePudding user response：

If you have a few kilobytes of memory available, you can eliminate this problem completely with a lookup table.

With a sampling period of 30 µs, 2500 samples will have a total duration of 75 ms. This is exactly equal to the duration of 21 cycles at 280 Hz.

I haven't tested or compiled the following code, but it should at least demonstrate the approach:

double sin2500() {
  static double *table = NULL;
  static int n = 2499;
  if (!table) {
    table = malloc(2500 * sizeof(double));
    for (int i=0; i<2500; i  ) table[i] = sin(2 * M_PI * 280 * i * 30e-06);
  }
  n = (n 1) % 2500;
  return table[n];
}

CodePudding user response：

How about a variant of others' modulo-based concept:

int t = 0;
int divisor = 1000000;
void control_loop() {
    t  = 30 * 280;
    if (t > divisor) t -= divisor;
    double sine = sin(2 * M_PI * t / (double)divisor));
    ...
}

It calculates the modulo in integer then causes no roundoff errors.

CodePudding user response：

I think it would be possible to use a modulo fmod() because sin() is periodic. Then you dont have to worry about the Problems.

double time = 0;
long unsigned int timesteps = 0;
double sine;
void controll_loop()
{
  timesteps  ;
  time  = 30e-6;
  time = fmod(time,1.0);
  sine = sin( 2 * M_PI * 280 * time );
  ...
}