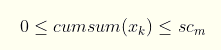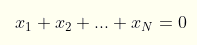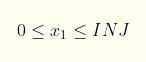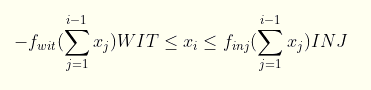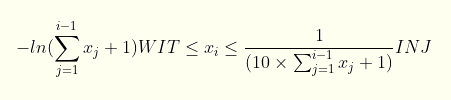Writing a function to optimize non-linear function nleqslv-CodePudding

I have a system of non linear equations I want to solve, but it I am finding it hard to write the function to optimize in nleqslv.

Here is what I want to do mathimatically; I want to minimize:

So the a values are constants and I want to search for the x values that minimize this sum.

The problem is the insane amount of constraints on the values I have. Which mathematically are, in order:

So, the cumulative sum of the xs has to always be bigger or equal to 0 and less or equal to scm if k<N

However, the cumulative sum of all the xs together has to be equal to 0:

Finally, each of the xi can be negative (except the first one) and is bound by a minimum and maximum value and these values are a function of the cumulative sum of all the xs before it:

I set up fake values in R, in order to solve an easy version of this problem:

a <- c(20, 34, 22, 27)
scm <- 9300
finj <- function(x, inj_max){
  (1/(10 * x 1)) * inj_max
}

fwit <- function(x, wit_max){
  log( x  1) * wit_max
}
INJ <- 4650
WIT <- 4650

These functions translate the last constraint into:

fn <- function(x){
  
  #(0 <= x1) can't be expressed - so I put it x1   0.0000001
  c(
    x[1] - scm,
    x[1]   0.0000001,
    x[1]   x[2] - scm,
    x[1]   x[2]   0.0000001,
    x[1]   x[2]   x[3] - scm,
    x[1]   x[2]   x[3]   0.0000001,
    x[1]   x[2]   x[3]   x[4],
    #now start inj/wit constraints
    x[2] * (10 * x[1]  1) - INJ,
    x[2]   log(x[1]  1) * WIT   0.0000001,
    x[3] * (10 * (x[1]   x[2])  1) - INJ,
    x[3]   log(x[1]   x[2]  1) * WIT   0.0000001,
    x[4] * (10 * (x[1]   x[2]   x[3])  1) - INJ,
    x[4]   log(x[1]   x[2]    x[3]   1) * WIT  0.0000001
    )
  
}

nleqslv(c(4650, -4650, 4650, -4650), fn)

I wrote this function also and tried to solve it but I got the error:

Error in nleqslv(c(4650, -4650, 4650, -4650), fn) : 
  Length of fn result <> length of x!

It's logical that I get this error since I have so many constraints, so I don't know how I can solve this optimisation problem or how I can rewrtie the constraints to not have this error.

CodePudding user response：

I don't think you want nleqslv, which is for systems of nonlinear equations. You are trying to minimize a single function with multiple arguments. optim from base R should work.

As for the constraints, each parameter is bounded with a minimum and maximum, but the bounds are sequentially dependent, which makes it a little trickier. One approach is to perform sequential transformations of the inputs into their allowable space. This allows the function to accept any real values as inputs because it will automatically transform them to meet the constraints. I used pnorm for the transformation.

The other thing to consider is that the problem has N - 1 degrees of freedom since sum(x) must be 0. The way to handle that is to pass only N - 1 paramters to the function to be optimized and then set x[N] to be -sum(x[-N]).

Here's some example code using your "fake values":

scm <- 9300
INJ <- 4650
WIT <- 4650

a <- c(20, 34, 22, 27)

fT <- function(xT) {
  # transforms the input values xT into values that meet the problem constraints
  x <- numeric(length(xT)   1)
  mini <- 0             # the minimum for parameter 1
  maxi <- min(scm, INJ) # the maximum for parameter 1
  x[1] <- (maxi - mini)*(pnorm(xT[1]))   mini # transform xT[1] to a value between mini and maxi
  xcumsum <- x[1]
  
  for (i in 2:length(xT)) {
    mini <- max(-xcumsum, -WIT*log(xcumsum   1))     # calculate the minimum for parameter i
    maxi <- min(scm - xcumsum, INJ/(10*xcumsum   1)) # calculate the maximum for parameter i
    x[i] <- (maxi - mini)*(pnorm(xT[i]))   mini      # transform xT[i] to a value between mini and maxi
    xcumsum <- xcumsum   x[i]
  }
  
  x[i   1] <- -xcumsum
  return(x)
}

fn <- function(xT) {
  return(sum(a*fT(xT)))
}

# optimize fn using a vector of N - 1 zeros as the initial guess
> optim(numeric(length(a) - 1), fn)
$par
[1]  17.3 -23.2   9.2

$value
[1] -88350

$counts
function gradient 
      32       NA 

$convergence
[1] 0

$message
NULL

The values returned by optim$par are transformed values. Invert the transform using fT:

x <- fT(optim(numeric(length(a) - 1), fn)$par)
> x
[1]  4650 -4650  4650 -4650

Passing x[1:3] to fn gives the minimized function value:

> fn(head(x, -1))
[1] -88350

Which checks out with calculating fn manually:

> sum(a*x)
[1] -88350