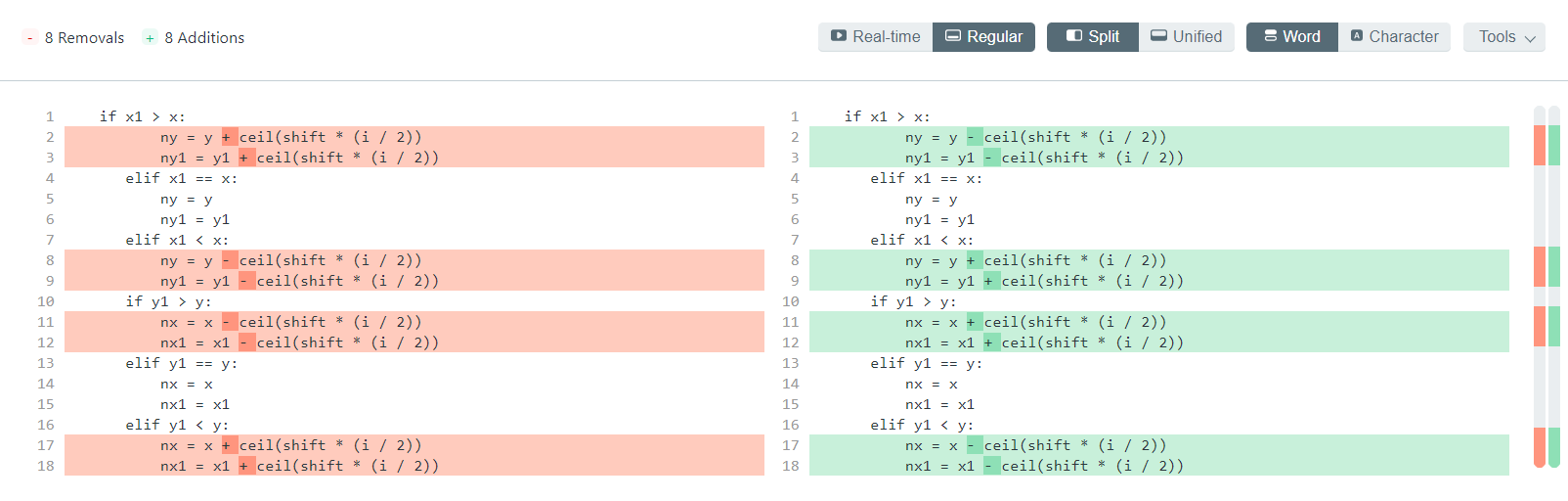
Here is my long if statement:
if i % 2 == 1 or i == 0:
if x1 > x:
ny = y ceil(shift * (i / 2))
ny1 = y1 ceil(shift * (i / 2))
elif x1 == x:
ny = y
ny1 = y1
elif x1 < x:
ny = y - ceil(shift * (i / 2))
ny1 = y1 - ceil(shift * (i / 2))
if y1 > y:
nx = x - ceil(shift * (i / 2))
nx1 = x1 - ceil(shift * (i / 2))
elif y1 == y:
nx = x
nx1 = x1
elif y1 < y:
nx = x ceil(shift * (i / 2))
nx1 = x1 ceil(shift * (i / 2))
else:
if x1 > x:
ny = y - ceil(shift * (i / 2))
ny1 = y1 - ceil(shift * (i / 2))
elif x1 == x:
ny = y
ny1 = y1
elif x1 < x:
ny = y ceil(shift * (i / 2))
ny1 = y1 ceil(shift * (i / 2))
if y1 > y:
nx = x ceil(shift * (i / 2))
nx1 = x1 ceil(shift * (i / 2))
elif y1 == y:
nx = x
nx1 = x1
elif y1 < y:
nx = x - ceil(shift * (i / 2))
nx1 = x1 - ceil(shift * (i / 2))
return nx, ny, nx1, ny1
I'm not sure if it's possible to just convert this whole thing into a simple equation. However, if not, is there any possible way to only have the first large if statement and make the sign in ny = y ceil(shift * (i / 2)) be plus if i % 2 == 1 or i == 0 and minus else?
CodePudding user response:
This means that only the ceiling sign changes between branches. We can fix this by adding a new variable:
ceil_sign = 1 if i % 2 == 1 or i == 0 else -1
if x1 > x:
ny = y ceil_sign * ceil(shift * (i / 2))
ny1 = y1 ceil_sign * ceil(shift * (i / 2))
elif x1 == x:
ny = y
ny1 = y1
elif x1 < x:
ny = y - ceil_sign * ceil(shift * (i / 2))
ny1 = y1 - ceil_sign * ceil(shift * (i / 2))
if y1 > y:
nx = x - ceil_sign * ceil(shift * (i / 2))
nx1 = x1 - ceil_sign * ceil(shift * (i / 2))
elif y1 == y:
nx = x
nx1 = x1
elif y1 < y:
nx = x ceil_sign * ceil(shift * (i / 2))
nx1 = x1 ceil_sign * ceil(shift * (i / 2))
You can also move branches around:
ceil_sign = 1 if i % 2 == 1 or i == 0 else -1
if x1 > x:
ny = y ceil_sign * ceil(shift * (i / 2))
ny1 = y1 ceil_sign * ceil(shift * (i / 2))
elif x1 < x:
ny = y - ceil_sign * ceil(shift * (i / 2))
ny1 = y1 - ceil_sign * ceil(shift * (i / 2))
else:
ny = y
ny1 = y1
if y1 > y:
nx = x - ceil_sign * ceil(shift * (i / 2))
nx1 = x1 - ceil_sign * ceil(shift * (i / 2))
elif y1 < y:
nx = x ceil_sign * ceil(shift * (i / 2))
nx1 = x1 ceil_sign * ceil(shift * (i / 2))
else:
nx = x
nx1 = x1
This refactoring allow us to see even more differences: the first if and its elif also only changes the ceiling sign. Let's add another variable:
ceil_sign = 1 if i % 2 == 1 or i == 0 else -1
if x1 == x:
ny = y
ny1 = y1
else:
x_ceil_sign = 1 if x1 > x else -1
ny = y x_ceil_sign * ceil_sign * ceil(shift * (i / 2))
ny1 = y1 x_ceil_sign * ceil_sign * ceil(shift * (i / 2))
if y1 == y:
nx = x
nx1 = x1
else:
y_ceil_sign = 1 if y1 < y else -1
nx = x y_ceil_sign * ceil_sign * ceil(shift * (i / 2))
nx1 = x1 y_ceil_sign * ceil_sign * ceil(shift * (i / 2))
As @Barmar suggested, note that ceil_sign always appears with the ceil call. You can combine them just once:
ceil_sign = 1 if i % 2 == 1 or i == 0 else -1
ceil_value = ceil_sign * ceil(shift * (i / 2))
if x1 == x:
ny = y
ny1 = y1
else:
x_ceil_sign = 1 if x1 > x else -1
ny = y x_ceil_sign * ceil_value
ny1 = y1 x_ceil_sign * ceil_value
if y1 == y:
nx = x
nx1 = x1
else:
y_ceil_sign = 1 if y1 < y else -1
nx = x y_ceil_sign * ceil_value
nx1 = x1 y_ceil_sign * ceil_value
You can do the same move with the internal ceil_signs:
ceil_sign = 1 if i % 2 == 1 or i == 0 else -1
ceil_value = ceil_sign * ceil(shift * (i / 2))
if x1 == x:
ny = y
ny1 = y1
else:
x_ceil_sign = (1 if x1 > x else -1) * ceil_value
ny = y x_ceil_sign
ny1 = y1 x_ceil_sign
if y1 == y:
nx = x
nx1 = x1
else:
y_ceil_sign = (1 if y1 < y else -1) * ceil_value
nx = x y_ceil_sign
nx1 = x1 y_ceil_sign
Note that in both clauses, you're adding nothing on the if branch and adding *_ceil_sign in the else branch. Create another variable:
ceil_sign = 1 if i % 2 == 1 or i == 0 else -1
ceil_value = ceil_sign * ceil(shift * (i / 2))
x_factor = 0 if x1 == x else ((1 if x1 > x else -1) * ceil_value)
ny = y x_factor
ny1 = y1 x_factor
y_factor = 0 if y1 == y else ((1 if y1 < y else -1) * ceil_value)
nx = x y_factor
nx1 = x1 y_factor
As an additional refactoring, note that if a > b, sign(a - b) is equal to 1. You can use this to refactor the *_factor variables:
def sign(x):
return 0 if x == 0 else 1 if x > 0 else -1
ceil_sign = 1 if i % 2 == 1 or i == 0 else -1
ceil_value = ceil_sign * ceil(shift * (i / 2))
x_factor = 0 if x1 == x else sign(x1 - x) * ceil_value
ny = y x_factor
ny1 = y1 x_factor
y_factor = 0 if y1 == y else -sign(y1 - y) * ceil_value
nx = x y_factor
nx1 = x1 y_factor
Also note that, if a == b, sign(a - b) is equal to 0, which defines both *_factors:
def sign(x):
return 0 if x == 0 else 1 if x > 0 else -1
ceil_sign = 1 if i % 2 == 1 or i == 0 else -1
ceil_value = ceil_sign * ceil(shift * (i / 2))
x_factor = sign(x1 - x) * ceil_value
ny = y x_factor
ny1 = y1 x_factor
y_factor = -sign(y1 - y) * ceil_value
nx = x y_factor
nx1 = x1 y_factor
CodePudding user response:
Here are some hints on how to approach problems like this generally:
- Look for commonly repeated expressions, and name them.
Here, ceil(shift * (i / 2)) happens a lot. Let's name that:
offset = ceil(shift * (i / 2))
if i % 2 == 1 or i == 0:
if x1 > x:
ny = y offset
ny1 = y1 offset
elif x1 == x:
ny = y
ny1 = y1
elif x1 < x:
ny = y - offset
ny1 = y1 - offset
if y1 > y:
nx = x - offset
nx1 = x1 - offset
elif y1 == y:
nx = x
nx1 = x1
elif y1 < y:
nx = x offset
nx1 = x1 offset
else:
if x1 > x:
ny = y - offset
ny1 = y1 - offset
elif x1 == x:
ny = y
ny1 = y1
elif x1 < x:
ny = y offset
ny1 = y1 offset
if y1 > y:
nx = x offset
nx1 = x1 offset
elif y1 == y:
nx = x
nx1 = x1
elif y1 < y:
nx = x - offset
nx1 = x1 - offset
return nx, ny, nx1, ny1
- Use Python's simultaneous assignment to group related assignments.
This is pretty straightforward:
offset = ceil(shift * (i / 2))
if i % 2 == 1 or i == 0:
if x1 > x:
ny, ny1 = y offset, y1 offset
elif x1 == x:
ny, ny1 = y, y1
elif x1 < x:
ny, ny1 = y - offset, y1 - offset
if y1 > y:
nx, nx1 = x - offset, x1 - offset
elif y1 == y:
nx, nx1 = x, x1
elif y1 < y:
nx, nx1 = x offset, x1 offset
else:
if x1 > x:
ny, ny1 = y - offset, y1 - offset
elif x1 == x:
ny, ny1 = y, y1
elif x1 < x:
ny, ny1 = y offset, y1 offset
if y1 > y:
nx, nx1 = x offset, x1 offset
elif y1 == y:
nx, nx1 = x, x1
elif y1 < y:
nx, nx1 = x - offset, x1 - offset
return nx, ny, nx1, ny1
- Exploit symmetries and parallels. (The reason I make simple syntax tweaks like the simultaneous assignment first is that, by reducing the line count, we can bring symmetrical things visually closer together, and thus notice symmetry more easily.)
What I mean by a "symmetry" or "parallel" is that we do fundamentally the same thing with different variables (or a related thing with some small, patterned alteration). There are two of these here: first, there's the way that the code depends on the i % 2 == 1 or i == 0. We can quickly see that the effect of this - propagated through all the if/elif logic - is that when the condition is false, offset is subtracted where it would otherwise be added, and vice versa. We can use elementary algebra to simplify that, by simply replacing offset with -offset when the condition isn't met. Thus:
offset = ceil(shift * (i / 2))
if not(i % 2 == 1 or i == 0):
offset = -offset
if x1 > x:
ny, ny1 = y offset, y1 offset
elif x1 == x:
ny, ny1 = y, y1
elif x1 < x:
ny, ny1 = y - offset, y1 - offset
if y1 > y:
nx, nx1 = x - offset, x1 - offset
elif y1 == y:
nx, nx1 = x, x1
elif y1 < y:
nx, nx1 = x offset, x1 offset
return nx, ny, nx1, ny1
- Make algebraic simplifications.
Pattern recognition is useful here. We are doing three-way comparisons, and depending on that comparison we either add, subtract or don't use a given value. We could represent that "add, subtract or don't use" by instead multiplying our offset by 1, -1 or 0 respectively. If we extract that idea:
def threeway_compare(a1, a):
if a1 > a:
return 1
elif a1 < a:
return -1
return 0 # a1 == a
then we find the hidden symmetry (i.e., we did that kind of three-way comparison twice):
offset = ceil(shift * (i / 2))
if not(i % 2 == 1 or i == 0):
offset = -offset
y_offset = threeway_compare(x1, x)
ny, ny1 = y y_offset, y1 y_offset
# Since the changes made to the nx/nx1 values were reversed,
# we negate the comparison result before using it this way.
x_offset = -threeway_compare(y1, y)
nx, nx1 = x x_offset, x1 x_offset
return nx, ny, nx1, ny1
- Scrap everything and try a different approach.
Sometimes this is called for. In this particular case, using ceil in order to calculate an "adjustment" is a warning sign that something is going wrong. It might have been better to compute the nx etc. values directly, rather than computing x etc. and then having to adjust them in this way. Perhaps this indicates something wrong about the original question.