Why is str.replace so fast?-CodePudding

I'm currently learning and practicing algorithms on strings. Specifically I was toying with replacing patterns in strings based on KMP with some modifications, which has O(N) complexity (my implementation below).

def replace_string(s, p, c):
    """
    Replace pattern p in string s with c
    :param s: initial string
    :param p: pattern to replace
    :param c: replacing string
    """
    pref = [0] * len(p)

    s_p = p   '#'   s
    p_prev = 0
    shift = 0

    for i in range(1, len(s_p)):
        k = p_prev

        while k > 0 and s_p[i] != s_p[k]:
            k = pref[k - 1]

        if s_p[i] == s_p[k]:
            k  = 1

        if i < len(p):
            pref[i] = k

        p_prev = k

        if k == len(p):
            s = s[:i - 2 * len(p)   shift]   c   s[i - len(p)   shift:]
            shift  = len(c) - k

    return s

Then, I wrote the same program using built-in python str.replace function:

def replace_string_python(s, p, c):
    return s.replace(p, c)

and compared performance for various strings, I'll attach just one example, for string of length 1e5:

import time


if __name__ == '__main__':
    initial_string = "a" * 100000
    pattern = "a"
    replace = "ab"

    start = time.time()
    res = replace_string(initial_string, pattern, replace)

    print(time.time() - start)

Output (my implementation):

total time: 1.1617710590362549

Output (python built-in):

total time: 0.0015637874603271484

As you can see, implementation via python str.replace is light-years ahead KMP. So my question why is that? What algorithm does python C code use?

CodePudding user response：

While the algorithm might be O(N), your implementation does not seem linear, at least not with respect to multiple repetitions of the pattern, because of

 s = s[:i - 2 * len(p)   shift]   c   s[i - len(p)   shift:]

which is O(N) itself. Thus if your pattern happens N time in a string, your implementation is in fact O(N^2).

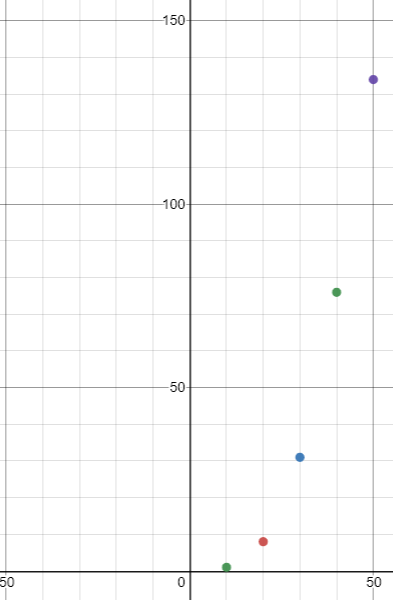
See the following timings for the scaling time of your algorithm, which confirms the quadratic shape

LENGTH  TIME
------------
100000    1s
200000    8s
300000   31s
400000   76s
500000  134s