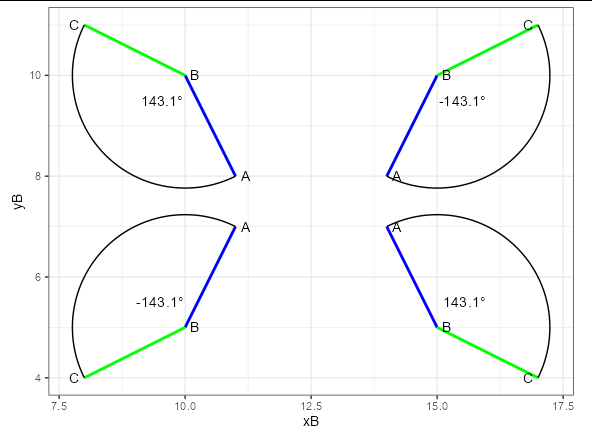
I can't get my head around the calculation of atan2 and placing a geom_arc on the intended side.

Here's some dummy data with four pairs of points ABC. I'd like to draw four arcs, each on the side with the smaller angle and print the angle degrees. Calculating angle dregrees works, but I'd need 1) some switch to correct the atan2 and/or 2) another switch to put the arc on the intended side. Just exchanging start and end has no effect.

tmp <- tibble(xA = c(11, 14, 11, 14), yA = c(8, 8, 7, 7),
              xB = c(10, 15, 10, 15), yB = c(10, 10, 5, 5),
              xC = c(8, 17, 8, 17), yC = c(11, 11, 4, 4))

tmp <- tmp %>%
  # dAB = distance between A and B (same as distance BC)
  mutate(dAB = sqrt((xA - xB)^2   (yA - yB)^2)) %>%
  mutate(dBC = sqrt((xB - xC)^2   (yB - yC)^2)) %>%
  # calculate atan AB for arc start
  mutate(arcAB = atan2(yA - yB, xA - xB)) %>%
  # calculate atan BC for arc end
  mutate(arcBC = atan2(yC - yB, xC - xB)) %>%
  # calculate angle degree
  mutate(arc_deg = round((arcBC * (180 / pi)) - (arcAB *  (180 / pi)), 1)) %>%
  mutate(arc_deg = case_when(
    arc_deg >  180 ~ arc_deg - 360,
    arc_deg < -180 ~ arc_deg   360,
    TRUE           ~ arc_deg)) %>%
  # calculate position for angle dreeg text
  mutate(xAC = (xA   xC) / 2) %>%
  mutate(yAC = (yA   yC) / 2)
tmp

ggplot(tmp)   
  geom_segment(aes(x = xB, xend = xA, y = yB, yend = yA), size = 1, col = "blue")  
  geom_segment(aes(x = xB, xend = xC, y = yB, yend = yC), size = 1, col = "green")  
  geom_text(aes(x = xB   0.2, y = yB), label = "B")  
  geom_text(aes(x = xA   0.2, y = yA), label = "A")  
  geom_text(aes(x = xC - 0.2, y = yC), label = "C")  
  geom_arc(aes(x0 = xB, y0 = yB, r = dAB, start = arcAB, end = arcBC))   # plus or minus 2*pi
  geom_text(aes(x = xAC, y = yAC, label = paste0(arc_deg, "°")))  
  coord_fixed()   theme_bw()

The code above only works for the bottom-right arc:

I've seen

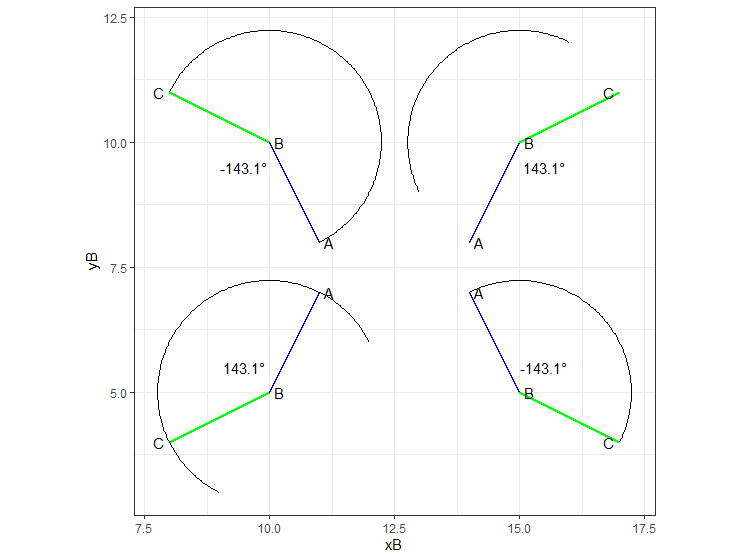
The key things here to realise are:

• As far as geom_arc is concerned, 0 degrees occurs on the y axis (at the 12 o'clock position) and positive angles are measured clockwise from there. Often when using trigonometric functions we would think of 0 degrees as being along the x axis and measured counter-clockwise. This is one of the assumptions behind atan2. What this means is that you need to calculate atan2 as atan2([delta x], [delta y]) rather than the other way round (the documentation says atan2([delta y], [delta x]), and this was the way your code had it).
• Since you wish to measure the smallest angle between the two lines, (i.e. the one less than pi radians) you need to find which of the differences between the angles are greater than pi radians, and in those cases add 2 * pi onto the smaller of the two angles. This ensures the angle is always below pi radians.