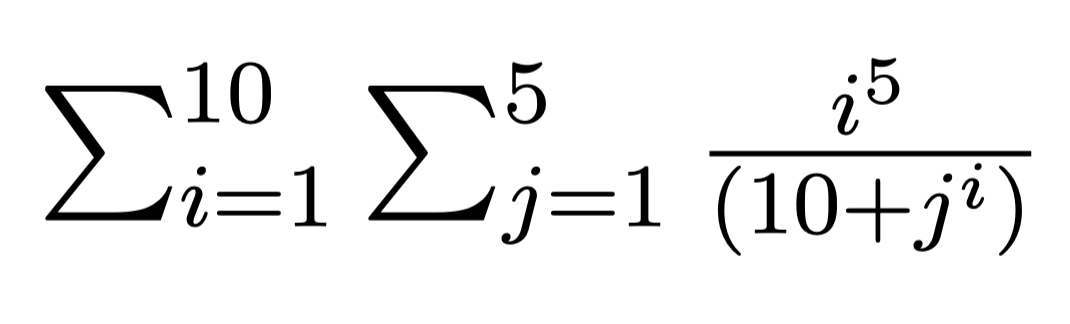Cumulative sums in R-CodePudding

I want to compute the following term in R, but without using loops ("for" cycles):

So far, I already calculated it manually and tried to use sequence functions for both index variables i and j and integrated them in a cumsum function and summed up the returning vector.

i <- seq(1:10)
j <- seq(1:5)

sum(cumsum((i^5)/(10 j^i)))

However, the results do not match with my manual calculation, so this seems to be a wrong approach. Could anybody help me out on this?

CodePudding user response：

Try outer

> sum(outer(1:10, 1:5, FUN = function(i,j) i^5/(10 j^i)))
[1] 20845.76

CodePudding user response：

Given

i <- seq(1:10)
j <- seq(1:5)

Solution 1:

ir <- rep(i, each = length(j))
jr <- rep(j, length(i))
sum(ir^5 / (10   jr^ir))
#> [1] 20845.76

Solution 2:

d <- expand.grid(i=i,j=j)
with(d, sum(i^5 / (10   j^i)))
#> [1] 20845.76

Solution 3: (@jogo)

sum(sapply(i, function(i) i^5 / (10 j^i)))
#> [1] 20845.76

CodePudding user response：

This is a fun programming challenge, so many different approaches possible!

solution 1

We can use the vectorized nature of arithmetic functions, i.e. (1:i)^2 runs fine.

i = 10L
j = 5L
sum((rep((1L:i)^5L, each = 5L) / ((rep.int(1L:j, j) ** rep(1L:i, each = 5L))   10L)))
#> [1] 20845.76

solution 2

Less elegant, with for-loop hiding through sapply

sum(matrix(rep.int((1L:i)^5L, 5L), ncol = 5) / (sapply(1L:j, \(.) .**(1L:i))   10L))

Benchmarks

Not that it matters - but for the curious among us:

bench::mark(
  Donald_one = {
    i = 10L
    j = 5L
    sum((rep((1L:i)^5L, each = 5L) / ((rep.int(1L:j, j) ** rep(1L:i, each = 5L))   10L)))
  },
  Thomas_one = {
    i = 10L
    j = 5L
    sum(outer(1L:i, 1L:j, FUN = function(i,j) i^5L/(10L j^i)))
  },
  Edo_one = {
    i <- seq(1:10)
    j <- seq(1:5)
    ir <- rep(i, each = length(j))
    jr <- rep(j, length(i))
    sum(ir^5 / (10   jr^ir))
  },
  Donald_two = {
    i = 10L
    j = 5L
    sum(matrix(rep.int((1L:i)^5L, 5L), ncol = 5) / (sapply(1L:j, \(.) .**(1L:i))   10L))
  },
  Edo_three = {
    i <- seq(1:10)
    j <- seq(1:5)
    sum(sapply(i, function(i) i^5 / (10 j^i)))
  },
  Edo_two = {
    i <- seq(1:10)
    j <- seq(1:5)
    d <- expand.grid(i=i,j=j)
    with(d, sum(i^5 / (10   j^i)))
  }
)[c(1, 3, 4, 5,6, 7)]

# A tibble: 6 x 6
  expression   median `itr/sec` mem_alloc `gc/sec` n_itr
  <bch:expr> <bch:tm>     <dbl> <bch:byt>    <dbl> <int>
1 Donald_one    7.8us   113744.    1.12KB    11.4   9999
2 Thomas_one   11.6us    82116.    1.36KB     8.21  9999
3 Edo_one      15.5us    62368.    1.36KB     6.24  9999
4 Donald_two     27us    32137.   12.02KB     9.64  9997
5 Edo_three    34.9us    27194.   19.57KB    10.9   9996
6 Edo_two      89.4us    10681.    2.09KB    10.5   5068