recursive ordered node coloring-CodePudding

I want to color all nodes of a given graph according to a given node ordering: the order is set through the Iterator<Node> nodeIterator parameter which contains all the nodes to process in the right order.

A node is colored if its neighbor is not and if a certain condition between the two considered nodes is met. A node is colored if it is an element of the parameter vector. A node is colored with its pre-defined color. an illustration of one example of coloring is here attached (nodes 1, 2 and 3 are in this specific order listed in the nodeIterator):

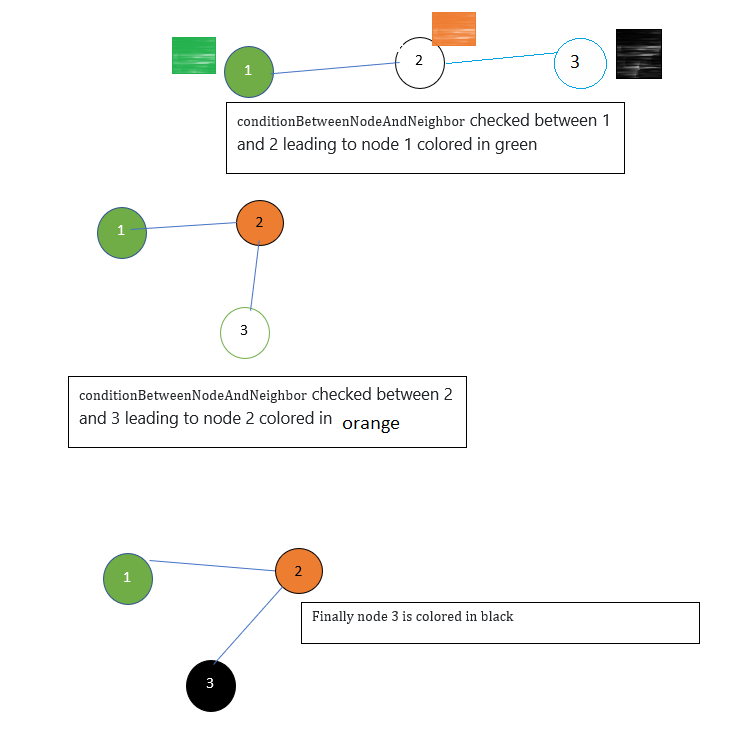
illustrating example of the node coloring

here's my code:

  #Recursive method colorNodes
    colorNodes(Graph graph,Iterator<Node> nodeIterator, Vector vector)
        if (vector.size() == graph.size())
            return true;
        node = nodeIterator.next();
        nodeNeighbors = node.getNeighbors();
        while(nodeNeighbors.hasnext()) {
            neighbor = nodeNeighbors.next();
            if (!nodeIsColored(vector, neighbor)) {
                if(conditionBetweenNodeAndNeighbor is true) {
                    vector.add(node) #color current node 
                    colorNodes(graph, nodeIterator,vector)#call recursively the method
                }
            }  
            else if (!nodeNeighbors.hasNext()) {
                    #potential last node or isolated node (having one neighbor only)
                  if(conditionBetweenNodeAndNeighbor is true) {
                    vector.add(node) #color last node anyway 
                    colorNodes(graph, nodeIterator,vector)#call recursively the method
                    }
                   }
            else {
                    continue;
                }
          return false;
        }

Could anyone clarify how to approach this problem and if my approach is correct (especially the cases differentiation)?

CodePudding user response：

I am not sure I fully understood the requirement. Please check this pseudo code:

    //Recursive method colorNodes
    colorNodes(Graph graph,Iterator<Node> nodeIterator, Vector vector){
        
        if (vector.size() == graph.size())   return true;
        node = nodeIterator.next();       
        neighbors = node.getNeighbors()
        
        //check if leaf or isolted or all neigbors colored 
        if( (! nodeIterator.hasNext())  or  (neighbor.length == 0)   or (allNodesAreColored(neighbors))  ) { 
            //color leaf 
            if(conditionBetweenNodeAndNeighbor is true) {
                vector.add(node) 
                node.setColor(color)
                // no need for recursive call for a leaf 
            }
            return;
        }
        
        for(neighbor : neighbors ){

            if ((!nodeIsColored(vector, neighbor) and
                    (conditionBetweenNodeAndNeighbor is true) ){
                    vector.add(node) 
                    node.setColor(color)
                    colorNodes(graph, nodeIterator,vector)
                    //break if you don't want to check rest of the neighbors 
             }
         }                      
     }

CodePudding user response：

I merely give an answer as the recursion is a bit awkward. I would expect the following - not regarding the logic.

// Recursive method colorNodes
void colorNodes(Graph graph, Iterator<Node> nodeIterator, List<Node> vector)
    //if (vector.size() == graph.size())
    //    return true;
    if (!nodeIterator.hasNext()) {
        return;
    }
    Node node = nodeIterator.next();
    if (nodeIsColored(vector, node)) {
        return;
    }               
    // Here the node is processed before the children, to stop recursion.
    vector.add(node);
    for (Node neighbor: node.getNeighbors()) {
        //if (!nodeIsColored(vector, neighbor)) {               
            colorNodes(graph, nodeIterator,vector);
        //}  
    }
    // Here the node could be processed after the children.
}

Vector<> is the old class, and still lives under that name in for instance C .