I am writing a function that recursively finds the minimum and maximum values in a binary tree and returns a tuple (min, max). My code is returning the correct min and max for my test case but separately. Any advice on how to get it to return a tuple is appreciated! (As a note, I am not allowed to use LinkedBinaryTree functions that iterate over the tree for me but I attached the class I am currently using under my code)

My code

from LinkedBinaryTree import LinkedBinaryTree


def min_and_max(bin_tree):

    if bin_tree is None:
        raise Exception("Tree is empty")

    def subtree_min_and_max(root):
        minval = root.data
        maxval = root.data
        if (root.left is None and root.right is None):
            temp = (minval, maxval)
            return temp
        elif (root.left is None):
            ltemp = subtree_min_and_max(root.right)
            if (ltemp[0] < minval):
                minval= ltemp[0]
            if (ltemp[1] > maxval):
                maxval = ltemp[1]
            temp = (minval, maxval)
            return temp
        elif (root.right is None):
            subtree_min_and_max(root.left)
            rtemp = subtree_min_and_max(root.right)
            if (rtemp[0] < minval):
                minval = rtemp[0]
            if (rtemp[1] > maxval):
                maxval = rtemp[1]
            temp = (minval, maxval)
            return temp
        else:
            ltemp = subtree_min_and_max(root.left)
            rtemp = subtree_min_and_max(root.right)
            print((min(root.data, ltemp[0], rtemp[0])))
            print(max(root.data, ltemp[1], rtemp[1]))
            temp = (min(root.data, ltemp[0], rtemp[0]), max(root.data, ltemp[1], rtemp[1]))
            return temp

    return subtree_min_and_max(bin_tree.root)

LinkedBinaryTree class

from ArrayQueue import ArrayQueue

class LinkedBinaryTree:

    class Node:
        def __init__(self, data, left=None, right=None):
            self.data = data
            self.parent = None
            self.left = left
            if (self.left is not None):
                self.left.parent = self
            self.right = right
            if (self.right is not None):
                self.right.parent = self

    def __init__(self, root=None):
        self.root = root
        self.size = self.count_nodes()

    def __len__(self):
        return self.size

    def is_empty(self):
        return len(self) == 0


    def count_nodes(self):
        def subtree_count(root):
            if (root is None):
                return 0
            else:
                left_count = subtree_count(root.left)
                right_count = subtree_count(root.right)
                return 1   left_count   right_count

        return subtree_count(self.root)


    def sum(self):
        def subtree_sum(root):
            if (root is None):
                return 0
            else:
                left_sum = subtree_sum(root.left)
                right_sum = subtree_sum(root.right)
                return root.data   left_sum   right_sum

        return subtree_sum(self.root)


    def height(self):
        def subtree_height(root):
            if (root.left is None and root.right is None):
                return 0
            elif (root.left is None):
                return 1   subtree_height(root.right)
            elif (root.right is None):
                return 1   subtree_height(root.left)
            else:
                left_height = subtree_height(root.left)
                right_height = subtree_height(root.right)
                return 1   max(left_height, right_height)

        if(self.is_empty()):
            raise Exception("Tree is empty")
        return subtree_height(self.root)


    def preorder(self):
        def subtree_preorder(root):
            if (root is None):
                pass
            else:
                yield root
                yield from subtree_preorder(root.left)
                yield from subtree_preorder(root.right)

        yield from subtree_preorder(self.root)


    def postorder(self):
        def subtree_postorder(root):
            if (root is None):
                pass
            else:
                yield from subtree_postorder(root.left)
                yield from subtree_postorder(root.right)
                yield root

        yield from subtree_postorder(self.root)


    def inorder(self):
        def subtree_inorder(root):
            if (root is None):
                pass
            else:
                yield from subtree_inorder(root.left)
                yield root
                yield from subtree_inorder(root.right)

        yield from subtree_inorder(self.root)


    def breadth_first(self):
        if (self.is_empty()):
            return
        line = ArrayQueue()
        line.enqueue(self.root)
        while (line.is_empty() == False):
            curr_node = line.dequeue()
            yield curr_node
            if (curr_node.left is not None):
                line.enqueue(curr_node.left)
            if (curr_node.right is not None):
                line.enqueue(curr_node.right)

    def __iter__(self):
        for node in self.breadth_first():
            yield node.data

My tester code

root = LinkedBinaryTree.Node(3)
T = LinkedBinaryTree(root)
a = LinkedBinaryTree.Node(2)
a.parent = root
root.left = a
b = LinkedBinaryTree.Node(7)
b.parent = root
root.right = b
c = LinkedBinaryTree.Node(9)
c.parent = a
a.left = c
d = LinkedBinaryTree.Node(5)
d.parent = c
c.left = d
e = LinkedBinaryTree.Node(1)
e.parent = c
c.right = e
f = LinkedBinaryTree.Node(8)
f.parent = b
b.left = f
g = LinkedBinaryTree.Node(4)
g.parent = b
b.right = g
print(min_and_max(T))

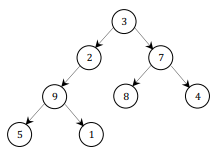
The tester code makes a tree that looks like

CodePudding user response：

In subtree_min_and_max, when the case root.right is None, your code do:

subtree_min_and_max(root.left)
rtemp = subtree_min_and_max(root.right)

Which should be a single

rtemp = subtree_min_and_max(root.left)

as at this time, the sub-tree has empty right children, and the procedure should search for min and max in the left children.