Find approximate value for the probability-CodePudding

I have made a simulation to following distribution:

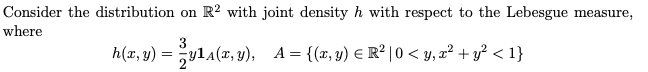
in the statistic program R and now I have to find a approximate value for the probability P(log(Y ) > sin(X)). How can I do that in R? Can anyone help me?

I hide my own simulation while other with same problem not should copy it. But I have this simulation from another post that also work:

n <- 1e4
X <- data.frame(x = runif(n, -1, 1), y = runif(n, 0, 1), z = runif(n, 0, 3/2))
i <- with(X, 0 < y & x^2   y^2 < 1 & z <= (3/2)*y) 
X <- X[i, ]

How can I for example use this simulation to find the probability P(log(Y ) > sin(X)) in R?

CodePudding user response：

I do not know how to post the solution without your mates are going to see it as well ... ;-)

# part 1: prepare probability density distribution on rect -1,...1
n <- 1e4
X <- data.frame(x = runif(n, -1, 1), y = runif(n, -1, 1), h=1)
X$h <- 3/2*X$y  # set probability density h = 3/2*y
head(X)

# part 2: restrict to half disk and normalize probability h to equal 1
i <- with(X, 0 < y & x^2   y^2 < 1) 
X <- X[i, ]
X$h <- X$h / sum(X$h)
plot(X[, 1:2], asp=1, pch='.')

# measure probability for points with log(y) > sin(x)
ii <- with(X, log(y) > sin(x))
points(X[ii, 1:2], pch='.', col="red")
p <- sum(X[ii, "h"])
p