Context: Convert an .iges to .vtk.

I have the following equation Ax^2 Bxy Cy^2 Dx Ey F=0 representing a conic section.

The parameters A~F are given. I want to find points on the conic section, so that I can connect them with lines, and make a mesh.

The reason I need the points instead of just using matplotlib Ellipse is because I'm creating a mesh not a plot.

It is in 3 dimension space, but I first get points on xy plane, and use affine transformation to send it to 3 dim.

Question: How do I find points given an implicit equation?

CodePudding user response：

To avoid spending too much time on this, I wrote some code that seems to handle general ellipses. It can be expanded for other conics, depending on what is needed. The code takes in the coefficients of a general quadratic equation of an ellipse and a number of desired points to be generated on the ellipse and generates a set of points on the ellipse.

import numpy as np

def equation(conic, points):
     '''
     equation of a conic with coefficients 'conic' 
     applied to a matrix number_of_points x 3 whose each row is the coordinates
     of each point
     '''
     c = np.array(conic)
     x = np.array([points[:,0]**2, points[:, 0]*points[:,1], points[:,1]**2, points[:,0], points[:,1], np.ones(points.shape[0])])
     return c.dot(x)
 
def equation_to_matrix(eq):
    '''
    eq[0]*x**2   eq[1]*x*y   eq[2]*y**2   eq[3]*x   eq[4]*y   eq[5] = 0
    '''
    return np.array([[2*eq[0],   eq[1],   eq[3]],
                     [  eq[1], 2*eq[2],   eq[4]],
                     [  eq[3],   eq[4], 2*eq[5]]]) / 2

def solve_quadratic(a, b, c):
    '''
    solves
    ax^2   bx   c = 0
    '''
    D = b**2 - 4*a*c
    D = np.sqrt(D)
    return (-b-D)/(2*a), (-b D)/(2*a)

def eigen2(S):
    '''
    solves the eigen-decomposition problem
    for a 2x2 symmetric matrix
    '''
    k1, k2 = solve_quadratic(1, -S[0,0]-S[1,1], S[0,0]*S[1,1] - S[0,1]*S[1,0])
    u1 = np.array([-S[0,1], S[0,0]-k1, 0])
    u1 = u1 / np.sqrt(u1.dot(u1))
    u2 = np.array([-u1[1], u1[0], 0])
    return np.array([k1, k2]), np.array([u1, u2, np.array([0,0,1])]).T

def center(conic_matrix):
    center = np.linalg.solve(conic_matrix, np.array([0,0,1]))
    return center/center[2]
    
def find_rotation_and_translation(conic_matrix):
    '''
    conic = c[0]x^2   c[1]*xy   c[2]*y^2   c[3]*x   c[4]*y   c[5] = 0
    the result is rotation U such that U.T C U = diag
    '''
    k, U = eigen2(conic_matrix)
    U[:,2] = center(conic_matrix)
    return U, k

def find_transform(conic):
    C = equation_to_matrix(conic)
    U, k = find_rotation_and_translation(C)
    C = (U.T).dot(C.dot(U))
    C = - C / C[2,2]
    k = np.array([1/np.sqrt(C[0,0]), 1/np.sqrt(C[1,1]), 1])
    return U.dot(np.diag(k))

def generate_points_on(conic, num_points):
    '''
    conic = [c[0], c[1], c[2], c[3], c[4], c[5]]
    coefficients of the qudaratic equation:
    conic: c[0]x^2   c[1]*xy   c[2]*y^2   c[3]*x   c[4]*y   c[5] = 0
    result is the affine transformation (scaling, rotation, translation)
    that maps the unit circle to the ellipse defined by the coefficients
    'conic' 
    '''
    cos_ = np.cos(2*np.pi* np.arange(0, num_points)/ num_points)
    sin_ = np.sin(2*np.pi* np.arange(0, num_points)/ num_points)
    U = find_transform(conic)
    points = np.array([cos_, sin_, np.ones(num_points)])
    return ((U.dot(points)).T)[:,[0,1]]

'''
Test:
'''

'''
Ellipse with equation whose coefficients are in the list E.
The ellipse has semi-major axes 2 and 1,
it is rotated 60 deg from the horizontal,
and its center is at (1, 4)
'''   
E = [ 3.25,  -2.59807621, 1.75, -23.40192379, 6.89230485,   39.35769515]


'''
U maps points from unit circle to points on E
'''
U = find_transform(E)

print(U)

'''
the set of points on the ellipse E
'''
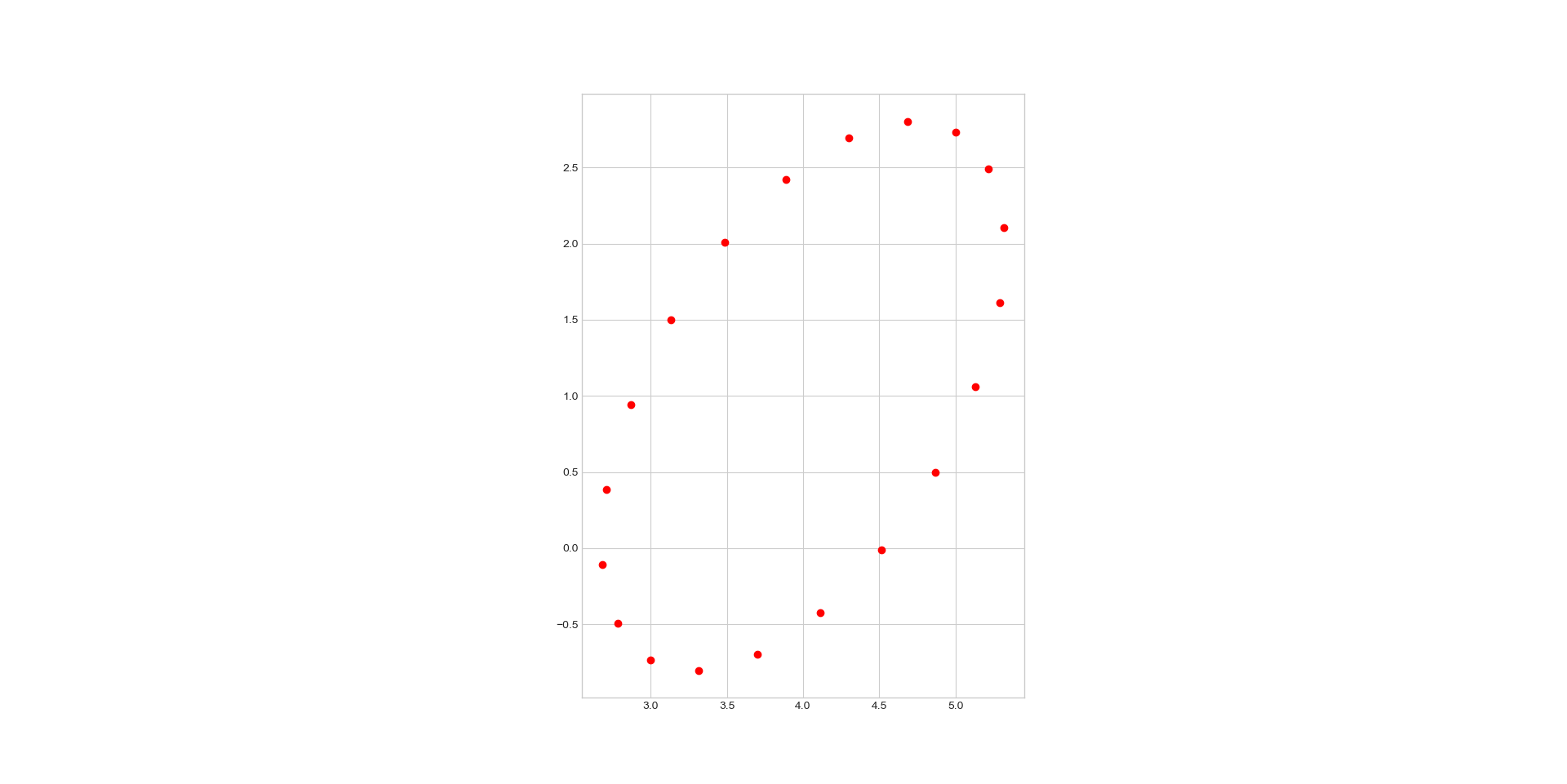
p = generate_points_on(E, num_points = 20)
print(p)


'''
check that the points p lie on the ellipse E
'''
print(equation(E, p).round(10))

'''
plot
'''
fig = plt.figure()
ax = fig.add_subplot()
ax.plot(p[:,0], p[:,1], 'ro')
ax.set_aspect('equal')
plt.show()