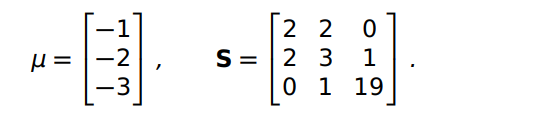Generate 200 data points drawn from a multivariate normal distribution with mean μ and covariance ma-CodePudding

import numpy as np
   from numpy import sin, cos, pi
   from matplotlib.pyplot import *
   rng = np.random.default_rng(42) 
   N = 200
   center = 10, 15
   sigmas = 10, 2
   theta = 20 / 180 * pi  
   # covariance matrix
   rotmat = np.array([[cos(theta), -sin(theta)],[sin(theta), cos(theta)]])
   diagmat = np.diagflat(sigmas)
   mean =np.array([−1,−2,−3])
   # covar = rotmat @ diagmat @ rotmat.T
   covar= np.array([[2, 2 ,0],[2 ,3, 1],[0, 1 ,19]])
   print('covariance matrix:')
   print(covar)`enter code here`
   eigval, eigvec = np.linalg.eigh(covar)
   print(f'eigenvalues: {eigval}\neigenvectors:\n{eigvec}')
   print('angle of eigvector corresponding to larger eigenvalue:',
      180 /pi * np.arctan2(eigvec[1,1], eigvec[0,1]))

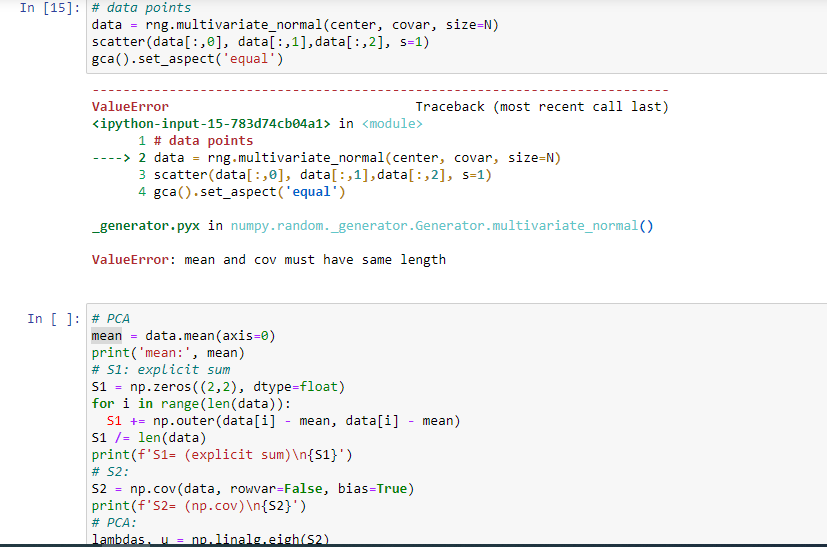after that I need to Perform PCA on the above data to one principal component and two principal components. What is the fractional explained variance in this two cases

CodePudding user response：

For generating the data, you need two tricks:

Compute a "square root" of covariance matrix S using eigenvalue-eigenvector factorization
Use the standard formula for generating a random normal with given mean and covariance. With Numpy it works on vectors (quoting from help(np.random.randn)):

For random samples from :math:`N(\mu, \sigma^2)`, use:

``sigma * np.random.randn(...)   mu``

Example:

import numpy as np

# Part 1: generating random normal data with the given mean and covariance
N = 200

# covariance matrix
S = np.array([[2, 2, 0], [2, 3, 1], [0, 1, 19]])

# mean
mu = np.array([[-1, -2, -3]]).T

# get "square root" of covariance matrix via eigenfactorization
w, v = np.linalg.eig(S)
sigma = np.sqrt(w) * v

# ready, set, go!
A = sigma @ np.random.randn(3, N)   mu

print(f'sample covariance:\n{np.cov(A)}')
print(f'sample mean:\n{A.mean(axis=1)}')


print(f'covariance condition number: {np.linalg.cond(S)}')
print('^^ note: this matrix is poorly conditioned; sample covariance will be noisy')

# Part 2: principal component analysis on random data A

# estimate the sample covariance
R = np.cov(A)
# do the PCA
lam, u = np.linalg.eig(R)

# fractional explained variance is the relative magnitude of
# the accumulated eigenvalues

# sort descending
col_order = np.argsort(lam)[::-1]
var_explained = lam[col_order].cumsum() / lam.sum()

print(f'fractional explained variance: {var_explained}')