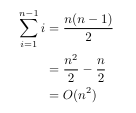For below code as there are 2 loops,so is it correct to say Time complexity is O(N) Square,because the code is in the form do this (which is second for loop ) each time for each element in first loop hence multiplying the run times

Is the understanding correct?

            const arr = [{ key1: 2 }, { key1: 7 }, { key1: 11 }, { key1: 15 }];
            const k = 9;
            let valueSet = new Set(arr.flatMap((x) => Object.values(x)));
            let valueArray = [...valueSet];

            let indices;
            let isFound = false;
            // valueArray.forEach((v1, i1) => {
            for (let i1 = 0; i1 < valueArray.length && !isFound; i1  ) {
              for (let i2 = i1   1; i2 < valueArray.length && !isFound; i2  ) {
                if ((valueArray[i1]   valueArray[i2]) === k) {
                  //Return the Indices
                  indices = [i1, i2];
                  isFound = true;;
                }
              }
            }
            console.log(indices);

Regards,

Carolyn

CodePudding user response：

Yes, you're right. In general, the double for-loop structure of your code produces O(n^2) time complexity, provided that you only do constant work inside the body of the inner for-loop, which in this case you are, as you only perform one check and possibly a couple assignments.

The O(n^2) complexity comes from the fact that you're effectively doing n-1 checks in your first inner for loop, n-2 in the second... 1 in the last, and the sum from 1 to n-1 is O(n^2):

This is of course the worst case complexity, where you look through every pair of values and don't find any pair summing to k, but generally it is the worst case you want to analyze when doing big O.

Looking at the complexity another way, you are generating all possible pairs of indices where the second index is greater than the first and doing constant work for each pair. There are n(n-1)/2 such possible pairs because you have n choices for the first index and n-1 choices for the second, but only half of those generated pairs will have the first index less than the second so you need to divide by two, producing the same exact n(n-1)/2 value as the sum.

As for the way you originally phrased the overall complexity in terms of "multiplying run-times", this is also correct but you have to be a little careful because the inner-loop run-time changes depending on which iteration of the outer-loop you're in. However, you could say that you're multiplying the run-time of the outer-loop, n, by the average run-time of the inner loop. The inner loop run-time ranges uniformly from 1 to n-1, so it's mean run-time is 1/2(n-1), giving us the same n(n-1)/2 = O(n^2) overall run-time.