I am working on principal component analysis (PCA) in Python. For comprehension reasons, I want to implement it myself. For that, I create random data based on a given covariance matrix, so that I can play with different values and how the principal component behave. So this script is just for understanding and clarifying the PCA.

My understanding is, that the principal components (which are the eigenvectors of the covariance matrix) are always orthogonal to each other. This is what the following picture of Wikipedia also says:

The description of the Image from Wikipedia (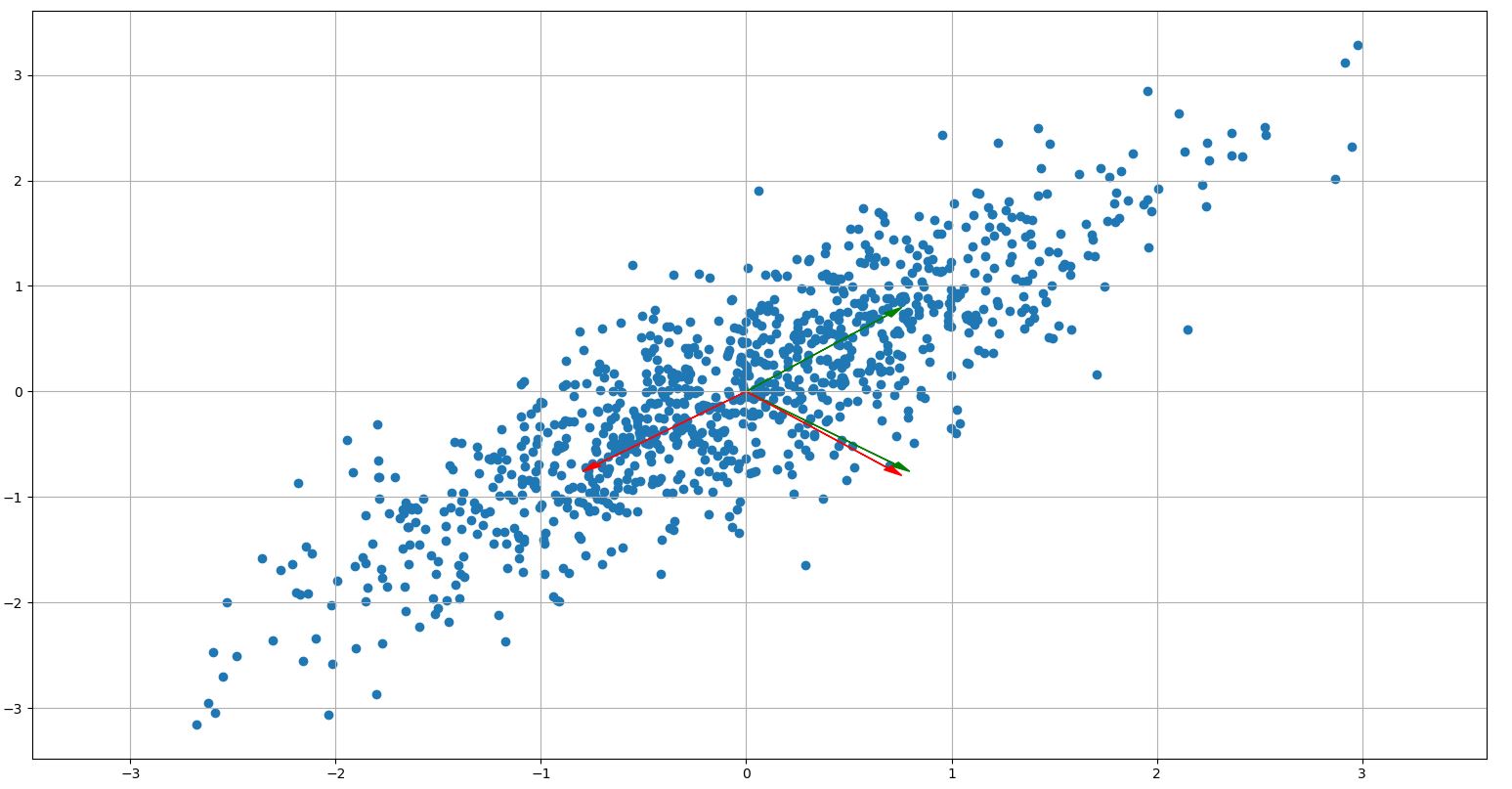

My Python script:

from matplotlib import pyplot as plt
import numpy as np
from sklearn.decomposition import PCA


def normalize(data: np.array, mean=None, std=None):
    """
    Normalize a pandas dataframe with respect to their stochastical moment. If mean and/or std is not passed they are
    calculated beforeheand.
    :param data:    Data to be normalized
    :param mean:    A mean value (optional)
    :param std:     A standard deviation (optional)
    :return:        normalized dataframe, mean value(s), standard deviation(s)
    """
    if mean is None:
        mean = data.mean(axis=0).reshape(1, -1)
    if std is None:
        std = data.std(axis=0).reshape(1, -1)

    res = data - mean / std

    return res, mean, std


# Press the green button in the gutter to run the script.
if __name__ == '__main__':
    datacount = 1000

    # create data based on given covariance matrix
    cov = np.array([[1, 0.85], [0.85, 1]])
    rand1 = np.random.multivariate_normal([1, 3], cov, datacount)

    # normalize, calculate covariance matrix and its eigenvectors and eigenvalues
    rand1, mean, std = normalize(rand1)
    cov = np.cov(rand1.T)
    eig_values, eig_vectors = np.linalg.eig(cov)

    # sort eig_values by importance and use this to also sort the vectors
    idx = np.argsort(eig_values, axis=0)[::-1]
    sorted_eig_vectors = eig_vectors[:, idx]

    # plot data
    plt.figure()
    plt.scatter(rand1[:, 0], rand1[:, 1])
    # set both axis limits to the maximum/minimum of the axis scalesv
    ax = plt.gca()
    xlimits = np.array(ax.get_xlim())
    ylimits = np.array(ax.get_ylim())
    axmax = np.max([np.max(xlimits), np.max(ylimits)])
    axmin = np.min([np.min(xlimits), np.min(ylimits)])
    ax.set_xlim([axmin, axmax])
    ax.set_ylim([axmin, axmax])

    # use PCA from sklearn for comparison
    pca = PCA(n_components=2)
    pca = pca.fit(rand1)

    # Plot the eigenvectors
    # Beware! Eigenvectors are oriented in rows in sklearn PCA and column-oriented in np.linalg.eig()!
    for i in range(2):
        plt.arrow(0, 0, pca.components_[0, i], pca.components_[1, i], color="g",
                  head_width=0.05, head_length=0.1)

    for i in range(2):
        plt.arrow(0, 0, eig_vectors[i, 0], eig_vectors[i, 1], color="r",
                  head_width=0.05, head_length=0.1)

    # plt.annotate(text='', xy=(1, 1), xytext=(0, 0), arrowprops=dict(arrowstyle='<->'))
    plt.grid()
    plt.figure()

    # Transform data to new subspace
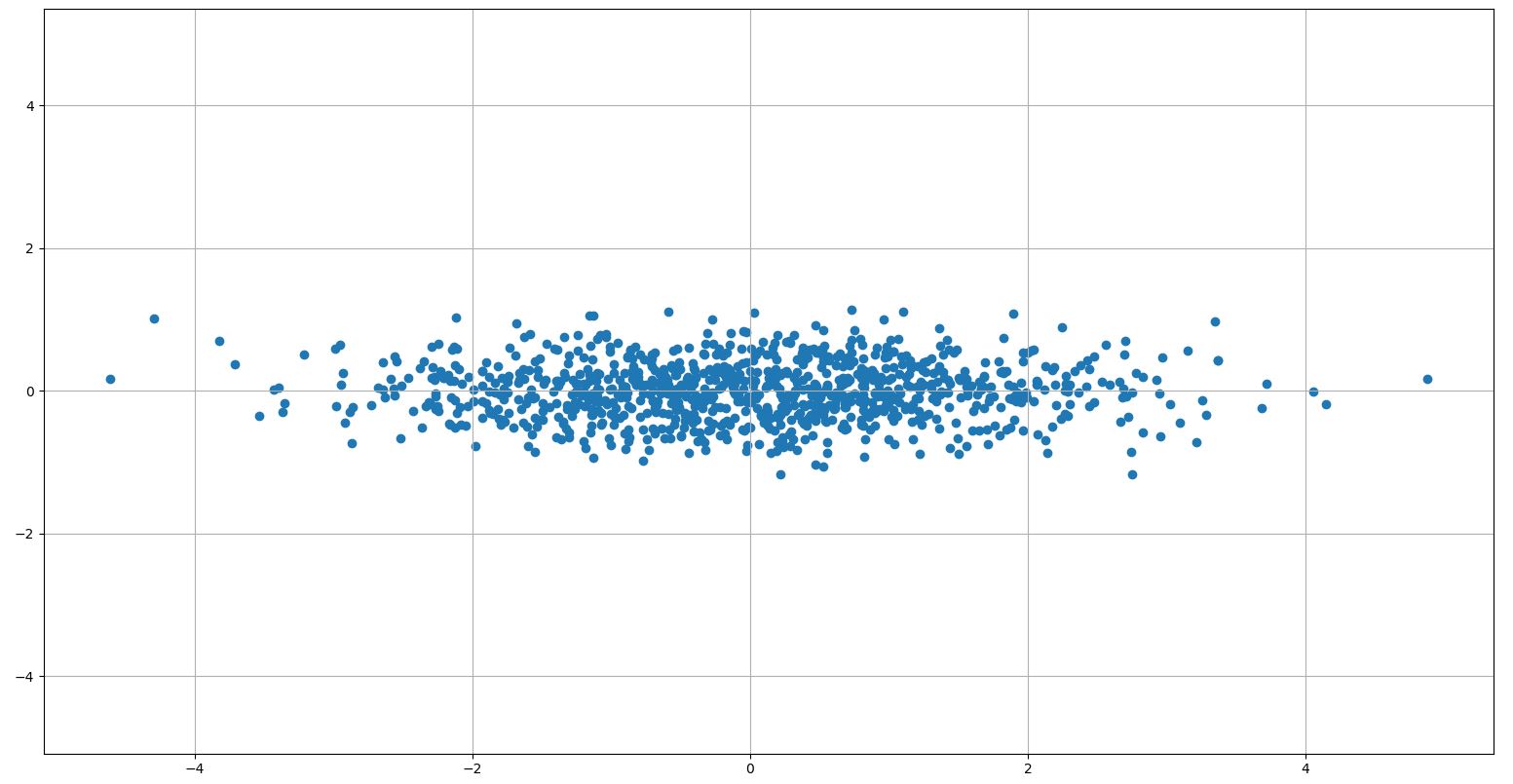
    eig_scores = np.dot(rand1, sorted_eig_vectors[:, :2]).T

    # plot PCAs in subspace
    plt.scatter(eig_scores[0], eig_scores[1])

    # set both axis limits to the maximum/minimum of the axis scales
    ax = plt.gca()
    xlimits = np.array(ax.get_xlim())
    ylimits = np.array(ax.get_ylim())
    axmax = np.max([np.max(xlimits), np.max(ylimits)])
    axmin = np.min([np.min(xlimits), np.min(ylimits)])
    ax.set_xlim([axmin, axmax])
    ax.set_ylim([axmin, axmax])
    plt.grid()
    plt.show()

    # Are Eigenvectors orthogonal?
    print(np.dot(eig_vectors[:, 0], eig_vectors[:, 1]) == 0)    # yields True
    print(np.dot(pca.components_[0, :], pca.components_[1, :]) == 0)    # yields True

Curiously the last two lines, where I check if the eigenvectors from both methods are orthogonal, always yield True, indicating that the vectors are in fact orthogonal.

Also the transformation of the data to the new subspace works fine with the following result:

What am I missing? Is my expectation false? Or is there a bug in my Python script?

CodePudding user response：

You checked that they are orthogonal, and they are, but in the plot you said they are not. Are the vectors plotted correctly? They are:

array([[ 0.707934  , -0.70627859],
       [ 0.70627859,  0.707934  ]])

looking at the figure it seems so.

The problem is that you are trying to measure the angle on your monitor, where the two axes have different scale.

Just add plt.axis('equal')