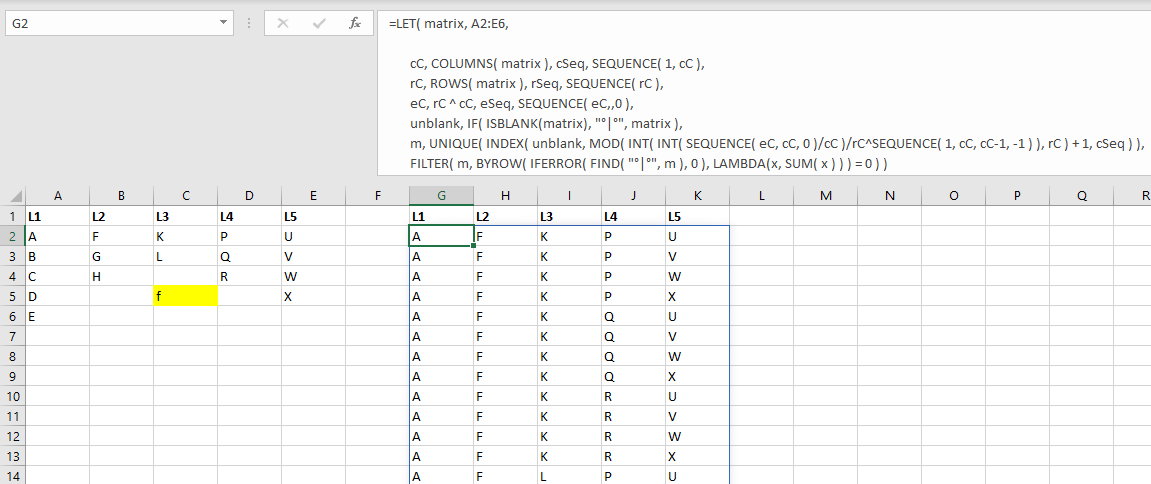
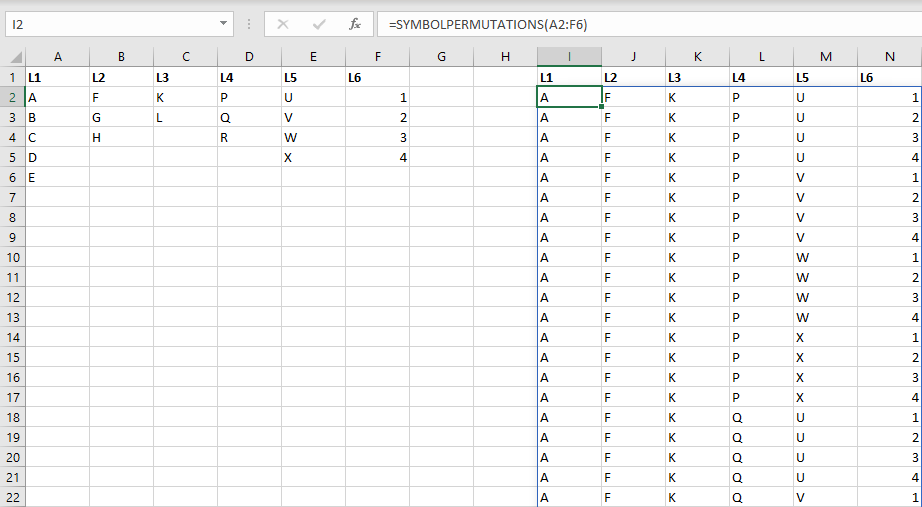
This is a frequently asked and answered question: how can I generate all permutations in Excel:

This formula inserts "°|°" in place of blanks so as to avoid having the blanks recast as 0's. It eliminates duplicates by applying UNIQUE.

This is super inefficient because it generates every possible permutation, including repeats and then filters them out. For a small scale matrix, it's not a big deal, but imagine that a 100 row by 3 column matrix would generate 1'000'000 rows and then filter them down to a small subset.

There is one small benefit, however, notice the f in the yellow cell, stranded in the middle of the column and not contiguous with its peers. This formula handles that like a champ. It just integrates it into the outputs of valid permutations. That will be important in the efficient formula below.

An Efficient General LET supported by LAMBDA

As for a general LAMBDA formula, I used:

SYMBOLPERMUTATIONS =
LAMBDA( matrix,

LET(
       cC, COLUMNS( matrix ),
       cSeq, SEQUENCE( 1, cC ),
       symbolCounts, BYCOL( matrix, LAMBDA(x, SUM( --NOT( ISBLANK( x ) ) ) ) ),
       rSeq, SEQUENCE( MAX( symbolCounts )-1 ),
       permFactors, INDEX( SCAN( 1, INDEX( symbolCounts, , cC-cSeq 1), LAMBDA(a,b, a*b ) ),, cC-cSeq 1 ),
       permMods, IFERROR( INDEX( permFactors,, IF( cSeq   1  > cC, -1, cSeq 1 ) ), 1 ),
       idx, INT( MOD( SEQUENCE( INDEX(permFactors, 1, 1),,0 ), permFactors )/permMods )   1,
       answer, INDEX( matrix, idx, cSeq ),
       er, OR( BYCOL( --ISBLANK(matrix), LAMBDA(x, SUM(--(INDEX(x,rSeq 1)<INDEX(x,rSeq))) ) ) ), // detect if there are stranded symbols
       IF( SUM(symbolCounts)=0, "no symbols",
             IF( er, "symbol columns must be contiguous",
                          answer ) ) )

)

This takes in matrix, just as above (the LET version is shown below). It delivers quite the same result, but there are significant differences:

• It is efficient. In the example shown here, the Simple formula above would generate 5^6 = 15625 permutations just to arrive at 1440 valid ones. This generates only what is needed and does not require filtering.
• However, it does not handle that stranded f at all. In fact, it would generate a 0 in the place of the f which is not something that a user with a ton of permutations might even notice.

For this reason, there is error detection and handling. The variable er detects if there are any stranded symbols in the matrix that are not column-wise contiguous with the ones above it using this LAMBDA Helper:

OR( BYCOL( --ISBLANK(matrix), LAMBDA(x, SUM(--(INDEX(x,rSeq 1)<INDEX(x,rSeq))) ) ) )

But this creates a new challenge and perhaps a whole new question. In the case of the stranded f, can anyone come up with a way to incorporate it?

The other error trap is to detect if the column is completely empty.

LAMBDA Magic

The magic that LAMBDA brings is from this one line that makes both formulas extensible to any number of columns without having to hard code them:

permFactors, INDEX( SCAN( 1, INDEX( symbolCounts, , cC-cSeq 1), LAMBDA(a,b, a*b ) ),, cC-cSeq 1 )

I got this from

=LET(A,A1:C3,B,ROWS(A),C,COLUMNS(A),D,B^C,E,MAKEARRAY(D,C,LAMBDA(rw,cl,INDEX(IF(A="","",A),MOD(CEILING(rw/(D/(B^cl)),1)-1,B) 1,cl))),FILTER(E,MMULT(--(E<>""),SEQUENCE(C,,,0))=C))

In short, what this does:

• Variables A-D are all helpers.
• The idea then is to just use simple INDEX()s to return all values. To do so we need the right indices for both rows and columns.
• MAKEARRAY() will make calculations relatively easy due to the recursive functionality that lambda brings. Inside these functions its basic math to return the correct indices for both these rows and columns. In fact there is no calculation needed for the columns as we simply refer to 'cl' and all the calculation for all the row indices is done through MOD(CEILING(rw/(D/(B^cl)),1)-1,B) 1.
• FILTER() and MMULT() work nicely together to filter out any unwanted results (read; empty).

That's as compact and quick as I think I could get this.