I encountered the LeetCode problem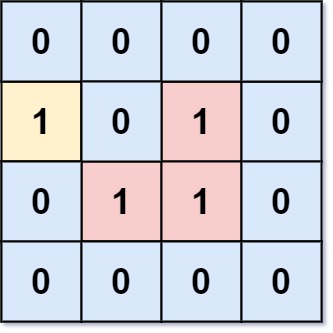

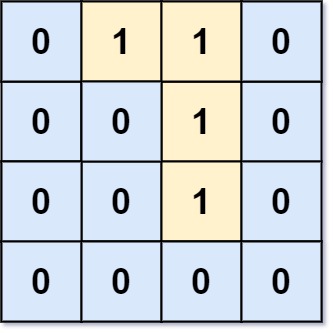
Input: grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
Output: 3
Explanation: There are three 1s that are enclosed by 0s, and one 1 that is not enclosed because its on the boundary.

Example 2:

Input: grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
Output: 0
Explanation: All 1s are either on the boundary or can reach the boundary.

I built the following solution using BFS

class Solution(object):
    def numEnclaves(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """

        stack = []
        visited = set()
    
        row_0 = grid[0]
        row_n = grid[-1]
        col_0 = [row[0] for row in grid]
        col_n = [row[-1] for row in grid]
    
        num_rows = len(grid)
        num_cols = len(grid[0])
    
        for col, val in enumerate(row_0):
            if val == 1:
                stack.append([0, col])
                visited.add((0, col))
            
        for col,val in enumerate(row_n):
            if val == 1:
                stack.append([num_rows-1, col])
                visited.add((num_rows-1, col))
    
        for row, val in enumerate(col_0):
            if val == 1:
                stack.append([row, 0])
                visited.add((row, 0))
    
        for row, val in enumerate(col_n):
            if val == 1:
                stack.append([row, num_cols -1])
                visited.add((row, num_cols -1))
           
        while stack:
            row, col = stack.pop(0)
            visited.add((row, col))
        
            steps = [[1, 0], [-1, 0], [0, 1], [0, -1]]
        
            for _row, _col in steps:
                _row  = row
                _col  = col
            
                if _row <0 or _row > num_rows -1:
                    continue
                
                if _col <0 or _col > num_cols -1:
                    continue
            
                if (_row, _col) in visited:
                    continue
                
                if grid[_row][_col] == 1:
                    stack.append([_row, _col])
    
        result = 0
        for row in range(1, num_rows-1):
            for col in range(1, num_cols -1):
                if grid[row][col] == 1 and (row,col) not in visited:
                    result  = 1
            
        return result
        

My solution works fine for smaller inputs, however it fails for larger values ex: a grid of size 200x200. I fail to understand what might be causing the TLE in the solution, or how I can optimise it further?

CodePudding user response：

Your solution is using a set in order to find if a node was visited - but this is not necessary since you can simply put a marker on the node saying you visited it. For example let's say 2 stands for visited from now on:

class Solution2(object):
    def numEnclaves(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """

        stack = []

        num_rows = len(grid)
        num_cols = len(grid[0])

        for row in range(len(grid)):
            if grid[row][0] == 1:
                stack.append((row, 0))
                # 2 means visited from now on
                grid[row][0] = 2

            if grid[row][num_cols - 1] == 1:
                stack.append((row, 0))
                grid[row][num_cols - 1] = 2

        for col in range(len(grid[0])):
            if grid[0][col] == 1:
                stack.append((0, col))
                grid[0][col] = 2

            if grid[num_rows - 1][col] == 1:
                stack.append((0, col))
                grid[num_rows - 1][col] = 2

        while len(stack) != 0:
            row, col = stack.pop(0)

            steps = [[1, 0], [-1, 0], [0, 1], [0, -1]]

            for _row, _col in steps:
                _row  = row
                _col  = col

                if _row < 0 or _row > num_rows - 1:
                    continue

                if _col < 0 or _col > num_cols - 1:
                    continue

                if grid[_row][_col] == 2:
                    continue

                if grid[_row][_col] == 1:
                    stack.append((_row, _col))
                    grid[_row][_col] = 2

        result = 0
        for row in range(1, num_rows - 1):
            for col in range(1, num_cols - 1):
                if grid[row][col] == 1:
                    result  = 1

        return result

The time drops dramatically and the tests you gave in the question still passes. You should know that a set access is not really O(1) if the set size is very big.

CodePudding user response：

The main issue is that you do not mark cells as visited the moment you put them on stack (which really is a queue). This means that the stack will have duplicate cells, which slows down the process.

As mentioned by others, you can use the grid itself for marking cells as visited, but I would just wipe out the 1 that you visit (to 0). Then at the end you only need to sum all cell values.

Some other things:

• Only define steps once, not inside the loop;
• Use sum to get the final count;
• Avoid putting corner cells twice on the initial queue
• Use operator chaining for checking that row and column are in range

Suggested code:

class Solution(object):
    def numEnclaves(self, grid):
        num_rows = len(grid)
        num_cols = len(grid[0])
    
        queue = [
            (0, col) for col, val in enumerate(grid[0]) if val == 1
        ]   [
            (num_rows-1, col) for col,val in enumerate(grid[-1]) if val == 1
        ]   [
            (row 1, 0) for row, val in enumerate(grid[1:-1]) if val[0] == 1
        ]   [
            (row 1, num_cols-1) for row, val in enumerate(grid[1:-1]) if val[-1] == 1
        ]
        for row, col in queue:
            grid[row][col] = 0
        steps = [[1, 0], [-1, 0], [0, 1], [0, -1]]
        while queue:
            row, col = queue.pop(0)        
            for _row, _col in steps:
                _row  = row
                _col  = col
                if 0 <= _row < num_rows and 0 <= _col < num_cols and grid[_row][_col] == 1:
                    grid[_row][_col] = 0
                    queue.append((_row, _col))

        return sum(sum(grid[row]) for row in range(1, num_rows-1))