Divergence between two timeseries in R-CodePudding

I have a data.table temp_dt which has index is x and two time series as y and z. Most of the time y and z move together but sometimes they disagree (and move in different directions). I want to create a new column, which shows the level of agreement (movement in the same direction) or level of disagreement (movement in different directions) between these two time series. I will appreciate it if someone can show me a better way to do so.

library(data.table)
temp_dt = structure(list(x = c(0, 1, 4, 5, 6, 7, 8, 11, 12, 13, 14, 15, 
18, 19, 20, 21, 22, 26, 27, 28, 29, 32, 33, 34, 35, 36, 39, 40, 
41, 42, 43, 46, 47, 48, 49, 53, 54, 55, 56, 57, 60, 61, 62, 63, 
64, 67, 68, 69, 70, 71, 74, 75, 76, 77, 78, 81, 82, 83, 84, 85, 
87, 88, 89, 90, 91, 92, 95, 96, 97, 98, 99, 102, 103, 104, 105, 
106, 109, 110, 111, 112, 113, 116, 117, 118, 119, 120, 123, 124, 
125, 126, 127, 130, 131, 132, 133, 134, 137, 138, 139, 140, 141, 
144, 145, 146, 147, 148, 151, 152, 153, 154, 158, 159, 160, 161, 
162, 165, 166, 167, 168, 169, 172, 173, 174, 175, 176, 179, 180, 
181, 182, 183, 186, 187, 188, 189, 190, 193, 194, 195, 196, 197, 
200, 201, 202, 203, 204, 207, 208, 209, 210, 211, 214, 215, 216, 
217, 218, 221, 222, 223, 224, 225, 228, 229, 230, 231, 232, 235, 
236, 237, 238, 239, 242, 243, 244, 245, 246, 249, 250, 251, 252, 
253, 256, 257, 258, 259, 260, 263, 264, 265, 266, 267, 270, 271, 
272, 273, 274, 277, 278, 279, 280, 281, 284, 285, 286, 287, 288, 
291, 292, 293, 294, 295, 298, 299, 300, 301, 302, 305, 306, 307, 
308, 309, 312, 313, 314, 315, 316, 319, 320, 321, 322, 323, 326, 
327, 328, 329, 330, 333, 334, 335, 336, 337, 340, 341, 342, 343, 
344, 347, 348, 349, 350, 351), y = c(1.51, 1.86, 6.04, 6.11, 
5.55, 10, 9.06, 0.99, 1.48, -0.77, 0.44, -0.37, -0.57, -0.64, 
-1.25, -0.72, -2.52, -2.65, -2.76, -2.76, -2.84, -2.13, -2.23, 
-2.27, -2.35, -2.48, -2.26, -2.38, -2.59, -2.59, -3.41, -3.34, 
-3.3, -2.56, -2.42, -1.3, -2.61, -2.61, -2.55, -1.92, -1.92, 
-1.98, -1.15, -2.05, -1.8, 0.07, -0.04, -0.07, -0.07, -0.87, 
-0.88, -0.99, -0.99, -0.99, -1.31, -1.5, -1.51, -1.65, -1.68, 
-1.95, -1.87, -1.87, -1.77, -4.01, -2.83, -2.84, -2.45, -2.98, 
-3.14, -4.77, -3.22, -3.11, -3.13, -3.08, -3.3, -3.51, -3.13, 
-4.9, -5.45, -6.26, -8, -4.97, -5.52, -5.69, -7.72, -8.17, -7.75, 
-7.22, -7.4, -7.31, -7.35, -7.16, -7.13, -4.96, -5, -5.06, -4.82, 
-4.86, -4.07, -4.97, -5.04, -2.96, -3.2, -0.96, -5.57, -3.84, 
-3.21, -5.59, -1.68, -3.17, -3.36, -3.36, -3.47, -2.77, -2.79, 
-3.69, -2.78, -2.8, -2.7, -1.19, -1.72, -1.88, -1.88, -2.13, 
-2.17, -2.17, -3.88, -4.05, -4.23, -4.32, -2.19, -2.35, -2.35, 
-1.08, -1.13, -1.37, -1.56, -1.59, -1.58, -0.22, 7.18, 6.42, 
-0.43, -0.46, -0.54, -1.1, -1.15, -0.99, -2.29, -1.19, -1.13, 
-1.13, -1.18, -2.69, -2.71, -2.75, -2.76, -2.85, -2.63, -3, -2.82, 
-4.09, -4.17, -5.99, -6.75, -3.54, -3.76, -4.66, -4.54, -4.58, 
-4.32, -4.38, -4.38, -4.44, -4.57, -4.36, -3.44, -3.51, -4.52, 
-3.6, -4.5, -3.54, -3.62, -3.78, -4.83, -4.1, -4.1, -4.19, -4.16, 
-4.19, -4.02, -4.06, -3.05, -3.14, -3.35, -3.39, -3.44, -3.51, 
-3.73, -4.7, -4.61, -7.45, -4.72, -4.74, -4.74, -4.63, -7.52, 
-7.61, -7.67, -7.57, -3.8, -4, -6.95, -6.95, -4.06, -6.98, -4.04, 
-7.23, -7.26, -4.04, -3.98, -7.28, -7.36, -7.38, -7.61, -7.42, 
-7.41, -7.57, -8.19, -8.45, -6.18, -6.26, -6.33, -6.42, -6.52, 
-7.58, -6.41, -7.9, -6.76, -8.27, -6.77, -6.82, -6.95, -6.25, 
-6.84, -6.8, -6.72, -6.08, -6.01, -6.4), z = c(11.17, 11.73, 
12.1, 12.815, 12.455, 14.49, 13.87, 11.905, 11.03, 10.6019, 10.91, 
10.95, 10.87, 10.465, 9.655, 9.039, 9.28, 7.79, 7.83, 7.83, 7.69, 
8.14, 8.83, 8.96, 8.61, 8.5, 8.95, 8.9, 8.36, 8.09, 7.9, 7.44, 
7.87, 8.07, 8.59, 8.02, 7.52, 7.83, 7.9, 7.9, 7.84, 7.91, 8.24, 
7.78, 7.78, 9.62, 9.28, 9.5, 9.77, 8.97, 8.52, 8.54, 8.6, 8.68, 
8.14, 8.14, 8.39, 8.83, 8.68, 8.47, 8.47, 8.44, 8.28, 6.99, 7.36, 
7.37, 7.54, 7.34, 7.34, 6.99, 7.33, 7.46, 7.56, 7.51, 7.19, 7.15, 
7.15, 6.7, 5.83, 5.32, 4.78, 5.53, 5.16, 5.1, 4.45, 3.67, 3.97, 
4.86, 4.5, 4.54, 4.84, 4.5, 4.99, 5.12, 5.31, 5.32, 5.77, 5.71, 
6.13, 5.86, 5.96, 5.62, 5.24, 5.16, 4.73, 5, 5.16, 4.51, 4.8, 
5.37, 5.63, 5.88, 5.67, 6.16, 6.21, 5.99, 6.1, 6.11, 6.98, 7.23, 
7.11, 7.4, 7.74, 7.41, 7.21, 7.16, 6.64, 6.76, 6.35, 6.25, 7.23, 
7.01, 7.25, 8.55, 8.92, 8.93, 8.95, 8.53, 8.58, 9.02, 10.27, 
10.11, 9.59, 9.81, 9.7, 9.68, 9.58, 9.58, 8.86, 9.08, 9.08, 9.26, 
9.17, 8.21, 8.46, 8.41, 8.12, 8.01, 8.71, 8.23, 8.15, 7.79, 7.45, 
6.03, 5.75, 6.15, 6.08, 5.96, 5.97, 5.89, 5.7, 5.53, 5.68, 5.58, 
5.79, 5.79, 6.29, 6.19, 5.72, 6.13, 5.83, 6.14, 6.33, 6.27, 5.86, 
5.54, 5.72, 5.9, 5.74, 5.63, 5.82, 5.99, 6.34, 6.81, 6.77, 6.57, 
6.72, 6.65, 6.26, 5.8, 5.56, 4.84, 5.31, 5.05, 5.27, 5.19, 4.97, 
4.46, 4.13, 4.23, 5.15, 5.12, 4.85, 4.73, 5.24, 4.81, 5.07, 4.81, 
4.87, 5.3, 5.3, 4.85, 4.86, 4.69, 4.35, 4.47, 4.5, 4.36, 3.51, 
3.36, 3.65, 3.49, 3.45, 3.23, 3.03, 2.95, 3.1, 2.58, 3.05, 2.99, 
3.23, 3.15, 3.45, 3.59, 3.52, 3.44, 3.66, 4.23, 4.57, 4.13)), row.names = c(NA, 
-250L), class = c("data.table", "data.frame"))

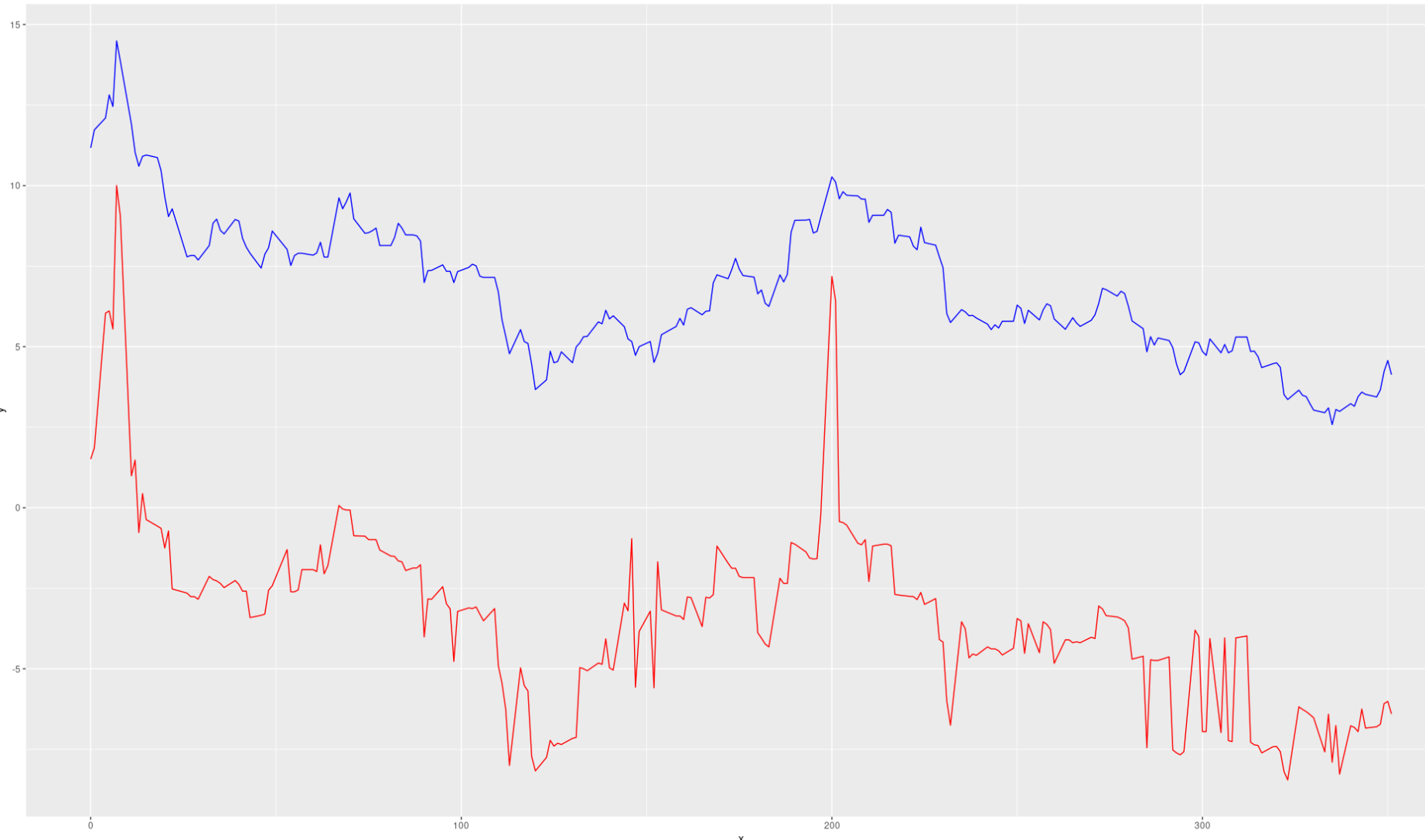
Here are the time-series -

library(ggplot2)
ggplot(na.omit(temp_dt ), aes(x))   
  geom_line(aes(y = y), color = "red")  
  geom_line(aes(y = z), color = "blue")

I have tried using RollingCorr function to spot changes in correlation between time-series, but it results in a very noisy time series and doesn't show if there is a convergence or divergence.

temp_dt[, div := RollingWindow::RollingCorr(y, z, window = 3, na_method = "ignore") * 10]

I want to create a time-series, which captures the convergence and divergence of y and z with more reliability.

CodePudding user response：

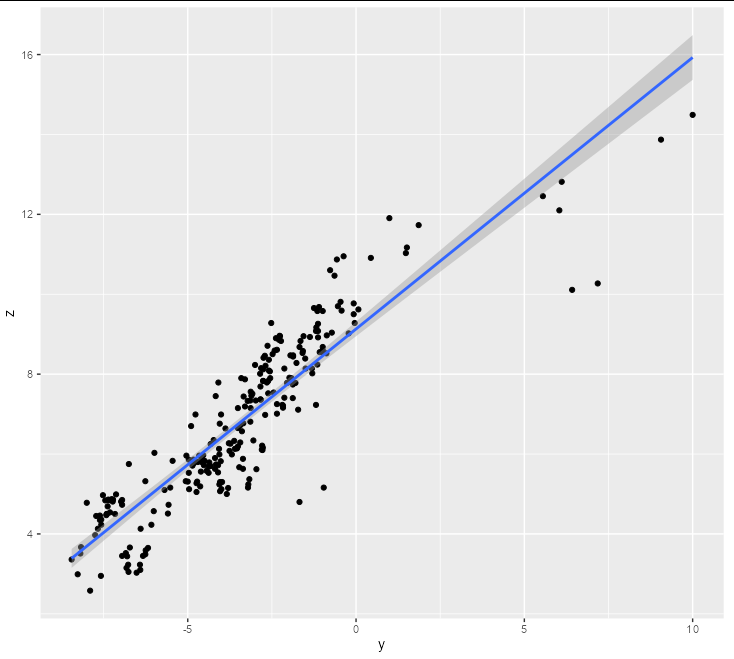
If you run a correlation and a regression of z and y, you will see that the two series are indeed closely related:

cor(temp_dt$y, temp_dt$z)
#> [1] 0.9011364

mod <- lm(z ~ y, data = temp_dt)
summary(mod)
#> Call:
#> lm(formula = z ~ y, data = temp_dt)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -3.7403 -0.5549  0.0870  0.6297  2.1267 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)  9.13065    0.09238   98.84   <2e-16 ***
#> y            0.67961    0.02076   32.73   <2e-16 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Residual standard error: 0.9407 on 248 degrees of freedom
#> Multiple R-squared:  0.812,  Adjusted R-squared:  0.8113 
#> F-statistic:  1071 on 1 and 248 DF,  p-value: < 2.2e-16

We can see this graphically by doing:

ggplot(temp_dt, aes(y, z))   geom_point()   geom_smooth(method = lm)

Finding the points where the two lines "disagree" is really just the same as finding the residuals of this model. It might be best, depending on your purposes, to use the squared residuals. This way you get a single measure of "disagreement", where numbers close to 0 indicate high agreement, and higher numbers indicate disagreement.

temp_dt$error <- mod$residuals^2

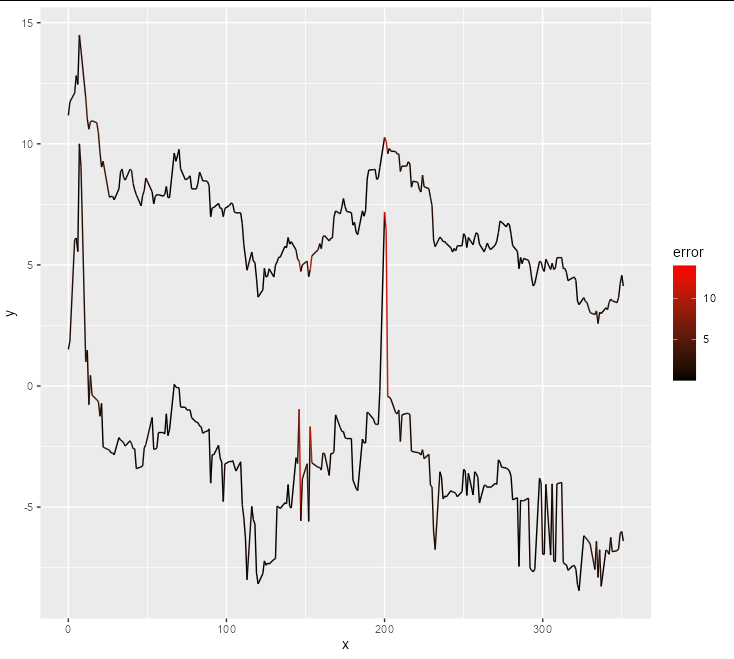
If you want to confirm this visually, we can make a plot where the lines turn red at points where they "disagree"


df <- data.frame(x = temp_dt$x,
                 x_end = c(tail(temp_dt$x, -1), tail(temp_dt$x, 1)),
                 y = temp_dt$y,
                 y_end = c(tail(temp_dt$y, -1), tail(temp_dt$y, 1)),
                 z = temp_dt$z,
                 z_end = c(tail(temp_dt$z, -1), tail(temp_dt$z, 1)),
                 error = temp_dt$error)

ggplot(df, aes(x, xend = x_end, colour = error))  
  geom_segment(aes(y = y, yend = y_end))  
  geom_segment(aes(y = z, yend = z_end))  
  scale_color_gradient(low = "black", high = "red")

CodePudding user response：

It is not clear what you mean by disagree. The easiest is just to calculate the difference like

temp_dt$difference = temp_dt$x - temp_dt$y

and see where it is far away from its own average.